Barisan deret aritmatika geometri, Hmmm…
Apa yang ada dalam pikiran teman-teman semua jika mendengar istilah barisan dan deret? Lalu apa juga yang langsung teman-teman pikirkan saat dengar aritmatika dan geometri?
Kalau saya pribadi;
- Ketika dengar barisan saya langsung ingat koma (,).
- Ketika dengar deret saya langsung ingat tambah (+).
- Ketika dengar aritmatika saya langsung ingat beda (b).
- Ketika dengar geometri saya langsung ingat rasio (r) atau pembanding.
Nah, bagaimana dengan teman-teman? Apakah sudah terbayang?
Jika belum, 4 poin yang sudah kak Hinda tuliskan di atas itulah ciri utama atau kata kunci dari pembahasan barisan dan deret, baik itu aritmatika maupun geometri.
Empat poin itu kemudian menjadi pembahasan yang cukup panjang dilengkapi dengan rumus-rumus yang akan kita bahas lengkap dalam kesempatan kali ini.
Saya yakin, ketika kalian sampai di artikel ini, berarti kalian sedang mencari tahu lebih banyak tentang barisan dan deret. Baik itu aritmatika (yang ditemukan oleh Carl Friedrich Gauss) maupun geometri (yang menurut beberapa sumber dikembangkan oleh Leonardo da Pisa).
Entah itu ciri-cirinya, perbedaan barisan dan deret, rumusnya, atau bahkan hanya untuk tahu bagaimana contoh soal berikut penyelesaian jawabannya.
Saya juga yakin, sebelum membaca artikel ini, kalian semua sudah memiliki pengetahuan dasar tentang barisan dan deret. Atau paling tidak pernah tahu atau mendengar istilahnya.
Baik itu dari buku sekolah maupun sumber lain.
Well, kita langsung saja ya!
Materi lengkap rumus barisan aritmatika, deret aritmatika, barisan geometri, dan deret geometri + contoh soal dan jawaban
Kita akan bahas materinya satu-satu ya?
1. Barisan Aritmatika
Pengertian barisan aritmatika adalah sebuah barisan bilangan yang memiliki selisih yang tetap atau konstan antara dua suku yang berurutan. Misal suku pertama dengan kedua, ketiga dengan keempat, dst.
Agar lebih mudah dipahami, kak Hinda akan menuliskan secara bertahap.
Bentuk umum dan rumus suku ke-n
Barisan aritmatika memiliki bentuk yang umum. Sebagaimana saya tuliskan di atas, ciri utamanya adalah koma. Setidaknya demikianlah cara saya memahami dengan mudah dan simpel tentang barisan aritmatika ini.
Bentuk umum:
a, a + b, a + 2b, a + 3b, …. , a + (n – 1)b
Keterangan:
- a adalah suku pertama dari barisan aritmatika.
- b adalah beda atau pembeda.
Biasanya,
- Suku pertama disebut juga dengan U1
- Suku kedua disebut U2
- Suku ketiga disebut U3
- …. dan seterusnya sampai
- Suku ke-n disebut Un
Dengan kata lain, barisan aritmatika bisa dituliskan sebagai berikut;
- U1, U2, U3, U4, … , Un = a, a + b, a + 2b, a + 3b, …. , a + (n – 1)b
Dari sini kita bisa melihat bahwa:
Rumus suku ke-n dari sebuah barisan aritmatika adalah :
Un = a + (n – 1)b
Keterangan:
- Un adalah rumus suku ke-n barisan aritmatika.
- a adalah suku pertama barisan aritmatika atau bisa ditulis U1
- b adalah beda
Rumus beda
Dengan ulasan di atas, kita dapat melihat;
- U2 – U1 = a + b – a = b
- U3 – U2 = a + 2b – (a + b) = b
- U4 – U3 = a + 3b – (a + 2b) = b
- …
- Beda = Un – Un-1 = a + (n-1)b – [a + (n-2)b] = a + bn – b – a – bn + 2b = b
Dengan demikian,
Rumus beda adalah:
b = Un – Un-1
Penjabaran a = U1
- Un = a + (n – 1) b
- U1 = a + (1 – 1) b
- U1 = a + 0.b
- U1 = a
Suku tengah
Dalam barisan aritmatika, kita juga mengenal suku tengah yang dilambangkan dengan Ut.
Apakah itu suku tengah?
Pengertian suku tengah ini merujuk pada sebuah barisan aritmatika yang n-nya ganjil. Atau dengan kata lain banyaknya barisan aritmatikanya ganjil.
Maka dengan begitu akan ada satu suku yang berada tepat di tengah dan membagi barisan aritmatika menjadi dua bagian yang sama.
Contoh:
- 1, 5, 9, 13, 17
- 2, 4, 6, 8, 10, 12, 14
Dari dua contoh barisan aritmatika di atas, terlihat bahwa 9 dan 8 merupakan suku tengah.
Kalau kita lihat bersama, bilangan 9 dalam barisan aritmatika pertama merupakan setengah dari penjumlahan suku-suku yang ada di kanan kirinya.
Demikian juga bilangan 8 di barisan aritmatika kedua.
- 9 = (5 + 13). ½ = (1 + 17) . ½
- 8 = (6 + 10) . ½ = (4 + 12) . ½ = (2 + 14) . ½
Perhatikan pula bahwa, suku tengahnya berada pada t = 3 dan t = 4.
Atau dengan kata lain;
Rumus t bisa dituliskan di bawah ini;
t = (n + 1) : 2
Pada contoh pertama, kita punya n = 5, suku tengahnya adalah suku ketiga.
- t = (5 + 1) : 2 = 6 : 2 = 3
Pada contoh kedua, kita punya n = 7, suku tengahnya adalah suku keempat.
- t = (7 + 1) : 2 = 8 : 2 = 4
Sedangkan rumus umum suku tengah sendiri adalah;
Rumus suku tengah :
- Ut = (a + Un)/2
- t = (n + 1) / 2
dengan
- a adalah suku pertama
- n > 1 dan ganjil
Contoh soal dan pembahasan
Berikut ini adalah beberapa contoh soal yang bisa kak Hinda rangkum agar pemahaman tentang barisan aritmatika ini menjadi lebih mudah;
Contoh 1
Diketahui sebuah barisan aritmatika adalah sebagai berikut:
1, 2, 3, 4, 5, 6, 7, 8, …
Tentukan suku pertama, beda, dan suku ke-n barisan aritmatika tersebut!
Pembahasan:
- Suku pertama = U1 = a = 1
- Beda (b) = U2 – U1 = 2 – 1 = 1
- Un = a + (n – 1)b
- Un = 1 + (n – 1).1
- Un = 1 + n – 1
- Un = n
Jadi, rumus suku ke-n dari barisan aritmatika di atas adalah n
Dalam contoh ini, U1 atau a adalah 1 dan beda (b) dalam barisan aritmatika ini adalah 1.
Contoh 2
Diketahui sebuah barisan aritmatika adalah sebagai berikut:
3, 7, 11, 15, …
Tentukan suku pertama, beda, dan suku ke-20!
Jawaban:
- Suku pertama = U1 = a = 3
- Beda = U2 – U1 = 7 – 3 = 4
Selanjutnya, untuk mencari suku ke-20 kita bisa memakai rumus suku ke-n;
- Un = a + (n – 1) b
- U20 = 3 + (20 – 1). 4
- U20 = 3 + 19. 4
- U20 = 3 + 76
- U20 = 79
Atau teman-teman bisa menghitung U20 dengan cara mencari rumus suku ke-n nya dulu seperti cara di bawah ini;
- Un = 3 + (n – 1) 4
- Un = 3 + 4n – 4
- Un = 4n – 1
Kemudian baru masukkan 20 ke dalam rumus suku ke-n yang sudah didapatkan; dengan cara;
- U20 = 4. 20 -1
- U20 = 80 – 1
- U20 = 79
Perlu diingat bahwa n adalah bilangan asli, tidak mungkin nol dan negatif.
Selain itu, kesalahan menghitung juga biasanya banyak dijumpai dalam pengerjaan soal barisan aritmatika yang sederhana.
Contoh kesalahannya adalah sebagai berikut;
- Un = a + (n – 1) b
- U20 = 3 + (20 – 1). 4
- U20 = 3 + 19. 4
Sampai di proses ini kadang banyak siswa yang menjumlahkan dulu. Padahal seharusnya perkalian harus didahulukan dibanding dengan penjumlahan. Kecuali jika ada kurungnya.
Contoh 3 – mencari suku pertama dari Un yang sudah diketahui
Diketahui rumus suku ke-n barisan aritmatika adalah:
Un = 2n + 1
Tentukan beda dan suku pertamanya!
Penyelesaian:
Diketahui: Un = 2n + 1, maka:
- Un-1 = 2 (n – 1) + 1
- Un-1 = 2n – 2 + 1
- Un-1 = 2n – 1
Kemudian, ingat bahwa rumus beda adalah:
- b = Un – Un-1
- b = 2n + 1 – (2n – 1)
- b = 2n – 2n + 1 + 1
- b = 2
Selanjutnya, cari suku pertamanya dengan memasukkan n = 1;
- Un = 2n + 1
- U1 = 2.1 + 1
- U1 = 2 + 1
- U1 = 3
Jadi, suku pertama dan beda dari barisan aritmatikanya adalah 3 dan 2.
Barisan aritmatika tersebut dapat ditulis sebagai berikut;
- 3, 5, 7, 9, 11, …., 2n + 1
Contoh 4 – suku tengah
Diketahui sebuah barisan aritmatika adalah sebagai berikut;
6, 10, 14, …, 46
Tentukan suku tengah dan suku ke berapakah suku tengah tersebut!
Pembahasan
Diketahui: a = 6, b = 4, Un = 46, maka:
- Ut = a + Un / 2
- Ut = (6 + 46) / 2
- Ut = 52/2 = 26
Kemudian, untuk mencari t, teman-teman bisa pakai rumus suku ke-n atau Un.
Un = a + (n – 1) b, karena n = t maka :
- Ut = a + (t – 1) b
- Ut = 6 + (t – 1) 4
- Ut = 6 + 4t – 4
- 26 = 4t + 2
- 4t = 26 – 2
- 4t = 24
- t = 24/4 = 6
Atau teman-teman juga bisa pakai cara di bawah ini:
- Un = a + (n – 1) b
- 46 = 6 + (n – 1).4
- 46 = 6 + 4n – 4
- 4n = 46 – 2
- 4n = 44
- n = 11
Kemudian masukkan dalam rumus:
- t = (n + 1) / 2
- t = (11 + 1) / 2
- t = 12/2 = 6
Hasilnya sama, bukan?
Tips dan trik barisan aritmatika
Ketika teman-teman diminta untuk mencari rumus suku ke-n dari sebuah barisan aritmatika. Langkah atau caranya adalah:
- Carilah terlebih dahulu suku pertama dan bedanya.
- Masukkan angka dalam rumus suku ke-n
- Ketika Anda diminta mencari suku ke-20, maka gantikan angka 20 pada bilangan n dari rumus yang Anda dapatkan tadi. Gantikan dengan bilangan lain sesuai dengan nilai n dalam soal.
Selanjutnya, jika teman-teman diminta untuk mencari nilai beda dan suku pertama dari sebuah rumus suku ke-n barisan aritmatika, maka langkahnya adalah:
- Cari rumus Un-1
- Kemudian masukkan ke rumus beda seperti biasa
- Untuk mencari suku pertama atau U1 bisa langsung dimasukkan dalam rumus suku ke-n yang diketahui dengan nilai n diganti 1.
Selanjutnya, jika teman-teman diminta untuk mencari nilai suku tengah dan nilai t, maka langkahnya adalah:
- Pakailah rumus Ut untuk menentukan suku tengahnya.
- Kemudian untuk mencari t, teman-teman bisa mencari nilai n, kemudian dimasukkan dalam rumus t = (n + 1) /2
- Lihat contoh di atas agar lebih jelas
2. Deret aritmatika
Deret identik dengan penjumlahan, sementara aritmetika identik dengan beda. Demikian saya memahami deret aritmatika agar tidak tertukar dengan barisan aritmatika atau deret geometri.
Kak Hinda akan membahas tentang materi deret aritmatika ini secara bertahap. Selamat menyimak.
Bentuk umum dan rumus
Sudah kakak jelaskan di awal bahwa deret identik dengan penjumlahan, sedangkan artimatika identik dengan beda.
Komponen dalam deret aritmatika ini hampir sama dengan barisan aritmatika, yaitu:
- Beda
- Suku pertama (U1 = a)
- Suku ke-n
Namun karena ini penjumlahan, maka ada komponen lain, yakni Sn.
Sebelumnya, mari kita kenali dulu bentuk umum dari deret aritmatika:
Bentuk umum
U1 + U2 + U3 + … + Un
a + (a + b) + (a + 2b) + … + [a + (n – 1) b]
Dalam deret aritmatika kita juga mengenal Sn, yakni jumlah n suku pertama deret aritmatika.
Rumus Sn adalah:
- Sn = n/2 (a + Un)
- Sn = n/2 [2a + ( n – 1 ) b]
Dengan:
- Un adalah rumus suku ke-n.
- Sn adalah jumlah n suku pertama dari deret aritmatika.
- b adalah nilai dari beda atau selisih.
- a adalah U1 atau suku pertama dalam barisan aritmatika.
Jika kalian lupa rumus a, b, dan Un bisa langsung lihat di ulasan barisan aritmatika sebelumnya ya?
Rumusnya sama.
Penjabaran rumus Sn
- Sn = U1 + U2 + U3 + … + Un
- Sn = a + (a + b) + (a + 2b) + … + [a + (n – 1) b]
- Sn = a + (a + b) + (a + 2b) + … + Un
- Sn = Un + (Un – b) + (Un – 2b) + … + a (dibalik dari Un – sifat komutatif)
Kemudian,
- Sn + Sn = [a + (a + b) + (a + 2b) + … + Un] + [Un + (Un – b) + (Un – 2b) + … + a]
- 2Sn = (a + Un) + (a + Un) + … + (a + Un) —-> sebanyak n kali
- 2Sn = n (a + Un)
- Sn = [n (a + Un) ] / 2
- Sn = n/2 (a + Un)
- Sn = n/2 {a + [a + (n – 1) b] }
- Sn = n/2 [2a + (n – 1) b]
Contoh dan pembahasan
Berikut adalah contoh soal dan jawaban deret aritmatika:
Contoh 1
Diketahui sebuah deret aritmatika; 5 + 7 + 9 + 11 +…
Tentukan rumus suku ke-n dan jumlah n suku pertamanya!
Pembahasan
Diketahui: a = 5, b = 2
- Un = a + (n – 1)b
- Un = 5 + (n – 1) 2
- Un = 5 + 2n – 2
- Un = 2n + 3
Rumus jumlah n suku pertamanya adalah:
- Sn = [n (a + Un) ] / 2
- Sn = (n (5 + 2n + 3)) / 2
- Sn = (5n + 2n2 + 3n)/2
- Sn = (2n2 + 8n) /2
- Sn = n2 + 4n
Contoh 2
Berikut adalah contoh kedua dalam materi deret aritmatika untuk mempermudah Anda dalam memahami materi ini:
Diketahui sebuah deret aritmatika:
4 + 5 + 6 + 7 + 8 + 9 +… ,
Tentukan suku ke- 10 dan jumlah 10 suku pertama dari deret tersebut!
Pembahasan
Diketahui, a = 4, b = 1. Maka:
Suku ke- 10 adalah
- Un = a + (n – 1) b
- U10 = 4 + (10 – 1) .1
- U10 = 4 + 9.1
- U10 = 13
Jumlah 10 suku pertama adalah
- Sn = n/2 (a + Un)
- S10 = 10/2 (4 + 13)
- S10 = 5 . 17
- S10 = 85
Jadi, suku ke 10 deret tersebut adalah 13 dan jumlah 10 suku pertama deret aritmatika tersebut adalah 85.
Tips dan trik deret aritmatika
Ketika teman-teman diminta untuk mencari rumus jumlah n suku pertama deret aritmatika, begini langkahnya:
- Cek nilai a dan b
- Masukkan dalam rumus suku ke-n
- Cari jumlah n suku pertama deret aritmatikanya.
Ketika teman-teman diminta untuk mencari suku ke-n dan n suku pertama deret aritmatika, maka langkahnya:
- Cek nilai a dan b
- Masukkan nilai n yang diminta ke dalam rumus suku ke-n. Misal n = 10, menjadi U10
- Masukkan nilai n yang diminta di soal ke dalam rumus jumlah n suku pertama deret aritmatika. Misal n = 10, maka carilah S10
- Agar jelas, silakan lihat contoh.
Latihan soal dan kuis deret aritmatika
Anda bisa mencoba mengerjakan deret berikut ini untuk mengasah kemampuan Anda;
- 6 + 10 + 14 + 18 + 22 + …
Silakan cari nilai:
- Suku pertama
- Beda
- Suku ke-7
- Jumlah 7 suku pertama deret aritmatika
- Suku ke-n
- Jumlah n suku pertamanya
Itulah materi deret aritmatika yang dapat kami sampaikan. Selanjutnya, kak Hinda akan mengajak teman-teman untuk membahas barisan dan deret geometri. Tapi jangan lupa baca juga Cara Menjumlahkan Deret Bilangan Berurut Tanpa Rumus Dengan Cepat.
3. Barisan geometri
Sebagaimana kak Hinda sebutkan di awal, barisan identik dengan koma, sedangkan geometri identik dengan rasio (pembagi).
Jadi, pembahasan kita nanti merupakan penjabaran dari materi barisan geometri yang sebenarnya sangat sederhana.
Untuk memahami materi ini, teman-teman harus paham dulu barisan aritmatika. Kenapa?
Barisan aritmatika terbilang lebih sederhana karena berhubungan dengan operasi hitung penjumlahan.
Sedangkan dalam barisan geometri sedikit lebih rumit karena menggunakan operasi hitung pembagian dan bahkan eksponensial.
Maka dari itu, materi ini biasanya disampaikan di tingkat sekolah menengah atas (SMA), MA (Madrasah Aliyah), dan SMK (Sekolah Menengah Kejuruan) sederajat.
Meski begitu, materi dasar barisan geometri ini kadang disinggung di bangku SMP. Hanya bagian dasarnya saja. Untuk SMA sederajat sudah materi yang lebih rumit lagi.
Kak Hinda akan membuat pembahasannya mudah dengan cara membaginya dalam beberapa poin. Yakni bentuk umum, rumus, penjelasan ringkas, dan contoh soal.
Selamat menyimak.
Bentuk umum dan rumus
Pengertian barisan geometri adalah sebuah barisan bilangan yang memiliki rasio atau hasil bagi tetap antara dua suku barisan yang tempatnya berurutan. Misal suku kedua dengan pertama, suku ketiga dengan kedua, dan seterusnya.
Geometri identik dengan rasio, dilambangkan dengan r. Barisan selalu pakai koma. Jadi, komponen dalam barisan geometri yang perlu diketahui adalah:
- Suku pertama (a = U1)
- Rasio (pembagi) dilambangkan dengan r
- Suku ke-n (Un)
Dengan kata lain, dalam barisan geometri kita tidak mengenal beda (b). Yang kita kenal adalah rasio (r).
Bentuk umum barisan geometri:
a, ar, ar2, ar3, …, arn-1
U1, U2, U3, U4, …Un
Dengan ulasan bentuk umum di atas, kita dapatkan:
Rumus suku ke-n barisan geometri:
- Un = arn-1
Keterangan:
- Un adalah suku ke-n
- a adalah suku pertama atau ditulis dengan U1
- r adalah rasio atau pembagi
Dari rumus Un di atas, kita bisa mendapatkan:
Rumus rasio barisan geometri:
- r = Un / Un-1
Berikut adalah penjabarannya:
- r = U2 / U1
- r = U3 / U2
- r = U4 / U3
- ….
- r = Un / Un-1
- dan seterusnya.
Contoh soal dan pembahasan
Berikut adalah beberapa contoh soal yang sengaja kak Hinda tulis secara bertahap tingkat kesulitannya agar teman-teman bisa mudah memahaminya.
Contoh 1
Diketahui sebuah barisan bilangan berikut:
- 2, 4, 8, 16, 32, …
Tentukan rasio dan suku ke-n barisan tersebut!
Pembahasan
Dari barisan tersebut, informasi yang kita dapat adalah:
- a = 2
- U2 = 4
Artinya:
- r = U2 / U1
- r = 4/2 = 2
Selanjutnya, suku ke-n atau Un adalah:
- Un = arn-1
- Un = 2 . 2n-1
- Un = 2 . 2n/2 ——–> Konsep eksponensial
- Un = 2n
Contoh 2
Jika diketahui, Un = 3n ,
Sebutkan 5 suku pertama dari barisan geometri tersebut dan tentukan rasio serta suku pertamanya!
Jawaban
Diketahui: Un = 3n
Jadi, untuk mencari 5 suku pertama dari barisan, kita tinggal memasukkan ke dalam rumus suku ke-n yang diketahui tersebut.
- U1 = a = 31 = 3
- U2 = 32 = 9
- U3 = 33 = 27
- U4 = 34 = 81
- U5 = 35 = 243
Lima suku pertama dalam barisan geometri ini adalah 3, 9, 27, 81, 243
Rasio :
- r = U2/U1
- r = 9/3
- r = 3
Atau teman-teman bisa mencari rasio dengan cara berikut ini;
- r = Un/Un-1
- r = 3n / 3n-1
- r = 3n : (3n/3) ———–> Konsep eksponensial
- r = 3n x (3/3n)
- r = 3
Perbedaan barisan geometri dengan barisan aritmatika
Perbedaan antara barisan geometri dengan barisan aritmatika adalah pada pembedanya. Jika di barisan aritmatika ada beda (selisih), di barisan geometri ada rasio (hasil bagi). Inilah kata kuncinya.
Berikut contohnya;
- 6, 12, 18, 24, … —–> Barisan aritmatika
- 4, 20, 100, 500, … ——> Barisan geometri
Bagaimana? Mudah, bukan?
Latihan soal barisan geometri
Jika Un = 2n-1.
Tentukanlah suku pertama, suku ke-12, dan rasionya!
Silakan menyelesaikan soal di atas dengan panduan materi barisan geometri di atas. Lakukan secara rutin agar terbiasa.
Tips dan trik barisan geometri
Kak Hinda akan memberikan tips dan trik untuk mengerjakan latihan soal di atas. Berikut langkahnya:
- Untuk mencari suku pertama jika rumus suku ke-n barisan geometri sudah diketahui adalah tinggal mengganti n dengan bilangan 1.
- Demikian juga dengan mencari nilai suku kedua belas, tinggal mengganti n dengan bilangan 12.
- Untuk mencari rasio, yang diperlukan adalah dua suku yang berurutan. Jadi, kalau sudah ada U1, kita tinggal mencari U2. Kemudian dicari hasil baginya.
Sebagai tambahan, untuk mengerjakan barisan geometri ini akan sangat mudah jika teman-teman paham materi eksponensial. Jadi, buka kembali bukunya di materi eksponensial ya?
4. Deret geometri
Materi deret geometri merupakan keberlanjutan dari materi barisan geometri. Ada yang menyebut deret geometri sebagai deret ukur.
Perbedaan mendasar barisan geometri dengan deret geometri adalah tanda penjumlahan. Dalam deret, kita akan diajak untuk menemukan hasil dari penjumlahan suku-sukunya.
Bentuk umum dan rumus
Simpelnya, komponen pembentuk deret geometri ini sama dengan barisan geometri, yaitu:
- Suku pertama (a)
- Rasio (r) – hasil bagi
- Suku ke-n (Un)
- Sn (jumlah n suku pertama)
Bentuk umum deret geometri :
- a + ar + ar2 + ar3 + … + arn-1
- U1 + U2 + U3 + U4 + … + Un
Untuk rumus-rumus a, r, dan Un, sama dengan rumus pada barisan geometri. Untuk di deret, kita mengenal Sn.
- Sn = U1 + U2 + U3 + U4 + … + Un
Rumus jumlah n suku pertama deret geometri :
- Sn = a (rn – 1) / r – 1 , untuk r > 1
- Sn = a (1 – rn) / 1 – r, untuk r < 1
Catatan: r tidak boleh sama dengan 1
Keterangan:
- Sn adalah jumlah n suku pertama dari deret geometri
- a = U1 adalah suku pertama
- r adalah rasio, yakni perbandingan dari dua suku yang berurutan, rumusnya r = Un / Un-1
Contoh dan pembahasan
Diketahui sebuah deret geometri sebagai berikut:
3 + 9 + 27 + 81 + …
Tentukan jumlah 6 suku pertama dan rumus Sn -nya!
Pembahasan
Diketahui:
- a = 3
- r = 9/3 = 3
Karena r > 1, maka digunakan rumus:
- Sn = a (rn – 1) / r – 1
- S6 = 3 . (36 – 1) / 3 – 1
- S6 = 3. (729 – 1) / 2
- S6 = 3. 728 / 2
- S6 = 2184 / 2 = 1092
Untuk mengetahui rumus Sn, gunakan cara:
- Sn = a (rn – 1) / r – 1
- Sn = 3 (3n – 1) / 3 – 1
- Sn = 3 (3n – 1) / 2
- Sn = 3n+1 – 3 /2
Latihan soal deret Geometri
Berikut adalah soal yang bisa coba Anda kerjakan. Sesuaikan soal di bawah ini dengan informasi di atas.
- 1 + 2 + 4 + 8 + …
- 5 + 25 + 125 + …
- 64 + 32 + 16 + 8 + 4 + 2 + 1 + ½ + ….
Tips dan trik deret geometri
Berikut adalah beberapa tips dan trik mengerjakan soal deret geometri berkaca dari pengalaman agar tidak banyak kekeliruan:
- Ketahui dulu berapa r nya.
- Setelah tahu rasionya, pastikan gunakan rumus yang tepat.
- Kunci utama rumusnya terletak pada bagian penyebut yang biasanya tidak boleh negatif. Kalau r lebih besar dari 1, maka r-1. Kalau r kurang dari 1, maka 1 – r. Silakan dilihat lagi.
- Jangan lupa menentukan nilai suku pertama.
- Memahami betul materi eksponensial atau perpangkatan akan sangat membantu.
- Sering berlatih soal.
Deret Geometri Tak Hingga
Bentuk umum deret geometri tak hingga adalah:
- a + ar + ar2 + ar3 +…
Keterangan:
- a adalah suku pertama, U1
- r adalah rasio
Deret geometri tak hingga terbagi menjadi dua, yakni konvergen dan divergen. Berikut adalah penjelasannya:
- Deret geometri tak hingga konvergen
Adalah sebuah deret yang memusat atau menuju ke satu titik tertentu (konvergen). Kekonvergenan deret geometri tak hingga bisa dilihat dari rasionya.
Deret geometri tak hingga dikatakan konvergen jika dan hanya jika harga mutlak r kurang dari 1. Atau ditulis:
- Konvergen <—> |r| < 1
Ketika deret geometri tak hingga itu konvergen, maka dia punya jumlah.
- Deret geometri tak hingga divergen
Adalah sebuah deret yang menyebar, bisa konstan, atau berisolasi. Dia tidak menuju ke satu titik tertentu.
Deret geometri tak hingga dikatakan divergen jika dan hanya jika harga mutlak r lebih dari atau sama dengan 1. Atau ditulis:
- Divergen <—> |r| ≥ 1
Ketika deret geometri tak hingga itu divergen, maka dia tidak memiliki jumlah.
- Ketika r = 1, maka deret geometri tak hingganya konstan.
- Ketika r > 1, maka suku-suku dalam deret geometri tak hingganya cenderung membesar dan menyebar.
Mengenali perbedaan konvergen dan divergen melalui contoh:
Bayangkan jika teman-teman diminta menghitung jumlah bilangan yang semakin membesar atau semakin mengecil ini ya?
- 6 + 36 + 216 + … (contoh deret geometri tak hingga divergen)
- 6 + 2 + 2/3 + 2/9 + … (contoh deret geometri tak hingga konvergen)
Deret geometri tak hingga yang memiliki jumlah adalah yang konvergen.
Rumus deret geometri tak hingga:
- S∞ = a / 1 – r
Dengan syarat -1 < r < 1
Keterangan:
- S∞ adalah jumlah deret geometri tak hingga.
- a adalah suku pertama
- r adalah rasio
Contoh deret geometri tak hingga konvergen
Diketahui sebuah deret sebagai berikut:
6 + 2 + 2/3 + 2/9 + …
Tentukan apakah deret tersebut konvergen dan berapa jumlahnya!
Pembahasan
Dari soal, kita bisa mendapatkan informasi:
- a = 6
- r = 2/6 = 1/3 —-> memenuhi syarat konvergen karena < 1
maka:
- S∞ = a / 1 – r
- S∞ = 6 / (1 – 1/3)
- S∞ = 6 / 2/3
- S∞ = 6 x 3/2
- S∞ = 9
Demikian informasi tentang materi deret geometri dan deret geometri tak hingga yang bisa kami paparkan. Semoga informasi ini bermanfaat untuk Anda serta dapat membantu Anda untuk memahami materi ini dengan mudah.
5. Kumpulan rumus
Berikut adalah ringkasan/rangkuman rumus barisan dan deret aritmatika, barisan dan deret geometri, serta deret geometri tak hingga:
Barisan dan deret aritmetika
- Un = a + (n – 1)b
- b = Un – Un-1
- Ut = (a + Un)/2
- t = (n + 1) / 2
- Sn = n/2 (a + Un)
- Sn = n/2 (2a + ( n – 1 ) b)
Barisan dan deret geometri
- Un = arn-1
- r = Un / Un-1
- Sn = a (rn – 1) / r – 1 , untuk r > 1
- Sn = a (1 – rn) / 1 – r, untuk r < 1
Deret geometri tak hingga
- S∞ = a / 1 – r
Dengan syarat -1 < r < 1
Ingat bahwa:
- Un adalah rumus suku ke-n.
- Sn adalah jumlah n suku pertama baik dari deret aritmatika maupun geometri.
- b adalah beda.
- a adalah suku pertama.
- r adalah rasio.
- Untuk suku tengah hanya bisa ada jika n ganjil dan lebih dari 1.
6. Contoh soal dan jawaban tingkat lanjut (Advanced)
Berikut adalah kumpulan contoh soal dan pembahasan barisan deret aritmatika geometri yang kita bahas kali ini.
Contoh soal di bawah ini sudah cukup rumit atau berada di tingkat advanced. Kalau ingin paham, sebaiknya pahami materi dasar dulu.
Contoh soal 1 – barisan aritmatika
Dalam sebuah barisan aritmatika, suku keempatnya adalah 14. Jika suku kedua dari barisan tersebut adalah 8, maka berapakah n jika suku terakhir dalam barisan tersebut adalah 23.
Jawaban
Dari soal, kita mendapatkan informasi:
U2 = 8 dan U4 = 14
Kita akan mencari Un dari informasi ini. Maka:
- U3 = (U2 + U4)/2 —-> ingat suku tengah
- U3 = 8 + 14 / 2
- U3 = 22 /2 = 11
Kemudian, kita cari b.
- b = U3 – U2
- b = 11 – 8 = 3
Karena b = 3, maka a = 8 – 3 = 5
Jadi, barisannya adalah:
5, 8, 11, 14, …, 23
Selanjutnya, kita akan mencari n dengan rumus;
- Un = a + (n-1) b
- 23 = 5 + (n-1) 3
- 23 = 5 + 3n – 3
- 23 = 2 + 3n (pindah ruas)
- 3n = 23 – 2
- 3n = 21
- n = 7
Dari sini, dapat diketahui bahwa banyaknya suku dalam barisan tersebut adalah 7 dan 23 adalah nilai dari suku ke-7 dari barisan aritmetika.
Contoh soal 2 – Barisan aritmetika SMPB SNMPTN
Contoh berikut merupakan jenis soal yang sering muncul di SMPB, SNAMPTN, SBMPTN, USM, Ujian Masuk, UMPTN, SNMPTN, atau saringan masuk perguruan tinggi negeri dan swasta.
Soal berikut adalah soal barisan aritmetika yang sebenarnya sederhana. Terlihat rumit karena angkanya yang cenderung besar.
Jumlah bilangan-bilangan bulat antara 250 dan 1.000 yang habis dibagi 7 adalah… (pilih salah satu jawaban)
- A. 45.692
- B. 66.661
- C. 73.775
- D. 80.129
- E. 54.396
Jawaban / pembahasan:
Bilangan bulat pertama yang habis dibagi 7 setelah 250 adalah 252, yakni menghasilkan angka 36.
Sedangkan angka terakhirnya sebelum 1000 adalah 994, yakni menghasilkan angka 142.
Artinya, barisan aritmetikanya adalah;
- 252, 259, 266, …., 994
Jadi, a = 252
Sedangkan suku ke-n adalah 994, maka:
- Un = a + ( n – 1 ) b
- Un = 252 + ( n – 1 ) 7
- 994 = 252 + 7n – 7
- 7n = 994 – 252 +7
- 7n = 749
- n = 749/7
- n = 107
Kemudian,
- Sn = ½ n ( a + Un ),
Maka:
- Sn = ½ . 107 (252 + 994)
- Sn = 53,5 . 1246
- Sn = 66.661
Kesimpulan:
Dengan demikian, jumlah bilangan-bilangan bulat antara 250 dan 1.000 adalah 66.661 (Jawaban B)
Contoh soal 3
Soal di bawah ini juga advanced dan biasa muncul di ujian saringan masuk perguruan tinggi;
Suku ke-n suatu deret aritmatika adalah Un = 3n – 5.
Tentukan rumus jumlah n suku pertama deret tersebut;
Pembahasan:
Diketahui Un = 3n – 5, maka
- a = U1
- a = 3 . 1 – 5
- a = – 2
Sehingga rumus jumlah n suku pertama,
- Sn = ½ n ( a + Un)
- Sn = ½ n (-2 + (3n – 5))
- Sn = ½ n ( -2 + 3n – 5)
- Sn = ½ n (3n – 7)
- Sn = n/2 (3n -7)
Soal ini lebih sederhana tapi sering sekali muncul di SPMB. Saat mengerjakan soal jenis ini lihat pilihan gandanya dulu.
Agar teman-teman bisa menyelesaikan sesuai dengan yang diinginkan soal di pilihan gandanya. Apakah harus diselesaikan sampai bentuk n2 atau tidak.
Demikian informasi tentang materi barisan dan deret aritmatika, barisan dan deret geometri, contoh soal dan pembahasannya. Semoga informasi dari kak Hinda ini bermanfaat ya?
Bacalah artikel ini sesuai dengan materi yang sedang teman-teman tempuh di sekolah ya? Agar tidak bingung.
Jangan lupa share jika bermanfaat. Selamat belajar.
Salam – hindayani.com

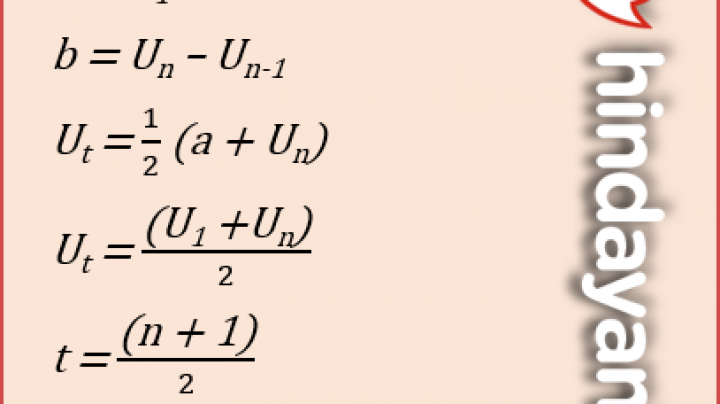









rikobonbal
terima kasih sudah mampir kak Riko! Selamat belajar
dikit niannnnnnnnnnn…..ap lahhh…nyeselllllll
Sudah diperbarui ya. 🙂 Sudah di tambah materi dan gambar ringkasan rumusnya.
Kurang banyak :G
Sudah diperbarui ya.. 🙂 Sudah ditambah dengan materi fresh dan gambar ringkasan rumus yang bikin betah baca..
SALAM SUKSES SEALLU
Siap..
Masih Bingung -_-
Materi yang mana yang masih bingung? Silakan ditanyakan. Barangkali bisa saya bantu jelaskan detailnya 🙂
gk paham
Tulisan ini sudah saya perbarui, silakan dibaca lagi barangkali bisa lebih paham. Atau kak Wahyu bisa tanya bagian yang masih gak dipahami ke saya. Akan saya bantu jelaskan.
contohnya kurang banyak, tolong ditambahkan agar lebih banyak bahan untuk latihan
Sudah diperbarui ya.. 🙂 Sudah ditambah dengan contoh dari tingkat mudah sampai tingkat mahir (advance)..
ksafhiuwfhkjsnf
Salam kak Syahrul. Semoga materinya membantu 🙂
:v
Terima kasih sudah mampir di situs hindayani.com kak Bagus… 🙂
Gk ngerti…..
Rulomahnya di mana…biar aku less
Saya di Malang kak Rafi… Kak Rafi dimana? Kalau misal jauh, bisa via situs ini saja dulu. Mana yang belum dimengerti? Agar saya perjelas. Silakan dibaca lagi, kontennya sudah diperbarui.
gitu aja gak ngerti payah
Terima kasih saya ucapkan sebelumnya sudah mampir di situs kami. Alhamdulillah kalau kak Abram sudah paham. Saya sarankan untuk tidak menggunakan kata kasar saat komentar.
o
gitu aja responnya…hemmm mendukung lah
Salam kak Maharani Dea… Makasih sudah belajar di hindayani.com
cukup paham,…teruslah berkarya …..good luck sistha
Yups, terima kasih. Semangat!
cukup bermanfaat terus berkarya dan jaya selalu
Terima kasih kak… Sukses juga untuk kakak… ^^
Tolong di jawab ya guys
BilaU6=56 dan
U10=97
Tentukan: a.Beda
b.U12
Kakak anggap ini soal aritmatika ya bukan geometri..
Rumus => Un = a + (n-1) b
-> U6 = 56
===> 56 = a + 5b
===> 56 – 5b = a
-> U10 = 97
===> 97 = a + 9b
===> 97 – 9b = a
-> a = a
===> 56 – 5b = 97 – 9b
===> 9b – 5b = 97 – 56
===> 4b = 41
===> b = 10,25 <----- pertanyaan (a) beda terjawab. Lanjut ke pertanyaan (b) -> Untuk mencari U12 harus dicari dahulu nilai a (suku pertama) dengan menggunakan data a dari U6, yaitu
->a = 56 – 5b
===> a = 56 – 5(10,25)
===> a = 56-51,25
===> a = 4,75
Sehingga,
-> U12 = 4,75 + (12-1) 10,25
===> U12 = 117,5 <------- pertanyaan b) U12 terjawab.
Sangat lengkap, membantu sekali. Terimakasih Kak Hinda!