Mari kita belajar tentang materi persamaan garis lurus, gradien, dan bagaimana menentukan apakah dua garis lurus itu tegak lurus atau sejajar.
Ulasan kita kali ini dimulai dari yang dasar berupa penjabaran materi yang berisi rumus, contoh soal dan jawaban persamaan garis tegak lurus, lalu dilanjutkan dengan latihan soal untuk dikerjakan di rumah.
Ayok kita mulai belajar bersama!
1. Menentukan Persamaan Garis Lurus yang Tegak Lurus, Sejajar, Melalui Titik, dan Diagram Kartesius
Sebelum kita membahas lebih jauh , terlebih dulu kakak berikan gambaran garis besar materi dalam daftar isi di bawah ini yang di dalamnya juga terdapat pengertian persamaan garis lurus dan juga contoh soal persamaan garis lurus SMP kelas 8 dan SMA kelas 11.
2. Persamaan garis lurus dan rumus gradien
Pada bagian awal ini kak hinda akan menerangkan apa itu gradien dan bagaimana bentuk persamaannya serta jenis dan contoh soalnya.
a. Pengertian gradien
Gradien adalah kemiringan garis.
Biasanya gradien dilambangkan dengan m.
b. Persamaan Gradien dalam garis lurus
Bentuk umum dari persamaan garis lurus adalah:
y = mx + c
Yang mana :
- m merupakan gradien,
- x dan y adalah variabel, dan
- c adalah konstanta.
Jika teman-teman menjumpai persamaan yang berbentuk:
ax + by + c = 0,
maka cara mencari gradien nya adalah:
- by = – ax – c
- y = (- ax – c) : b
- y = (- a/b)x – (c/b)
Jadi, rumus gradien nya adalah:
m = -a/b
c. Macam-macam gradien
Ada beberapa macam / nilai gradien yang perlu teman-teman tahu, di antaranya:
Gradien bernilai negatif
Contoh soal gradien negatif:
Diketahui sebuah persamaan garis lurus 4y + 2x – 8 = 0. Tentukan gradiennya!
Jawab:
m = -a/b = -2/4 = – ½
Jadi, gradiennya bernilai negatif.
Gradien bernilai positif
Contoh persamaan garis lurus:
Diketahui sebuah persamaan 3x – 2y + 6 = 0. Tentukan gradiennya!
Jawaban:
Rumus gradien : m = -a/b
Sehingga : -3/-2 = 3/2
Gradien yang melalui titik (0,0) atau pangkal koordinat
Jika sebuah garis lurus melalui titik pangkal, maka nilai gradiennya bisa dicari dengan cara:
m = y/x
Contoh latihan soal gradien:
Diketahui sebuah garis melalui pangkal koordinat dan titik (1,3). Berapakah gradiennya?
Pembahasan:
m= y/x = 3/1 = 3
Gradien garis yang melalui dua titik (x1, y1) dan (x2, y2)
Teman-teman bisa mencari gradien dari sebuah garis lurus hanya dengan mengetahui dua titik yang dilaluinya.
Misalnya sebuah garis lurus melalui titik A (x1, y1) dan B (x2, y2). Maka gradiennya dirumuskan sebagai:
m = [y2 – y1] : [x2 – x1]
Contoh:
Diketahui sebuah garis lurus melalui titik (2, 3) dan (1, -4). Berapakah gradiennya?
Jawab:
m = [y2 – y1] : [x2 – x1]
m = (-4 – 3) : (1 – 2)
m = -7 : -1
m = 7
3. Persamaan garis lurus yang sejajar
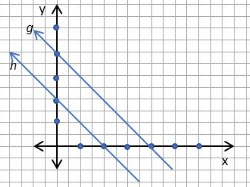
Silakan lihat gambar kartesius berikut untuk melihat ilustrasi dua buah garis lurus g dan h yang sejajar.
Dari gambar di atas kita bisa melihat dua buah garis lurus yang sejajar. Sepanjang apapun garisnya, keduanya tidak akan berpotongan.
Secara logika, dua persamaan garis lurus yang sejajar akan memiliki kemiringan garis yang sama. Dengan kata lain, kemiringan atau gradien dari dua garis tersebut adalah sama besar. Dan dituliskan sebagai berikut;
Misal y1 = m1x + c1 merupakan persamaan pertama dan y2 = m2x + c2 adalah persamaan kedua. Maka ketika dua garis ini sejajar berlaku;
m1 = m2
Artinya, gradien pada persamaan garis lurus pertama sama nilainya dengan gradien pada persamaan kedua.
a. Contoh soal persamaan garis sejajar:
Sebuah garis lurus memiliki persamaan 6y + 3x – 8 = 0. Tentukan gradien garis yang sejajar dengan persamaan tersebut!
b. Jawabannya:
Garis lurus pertama: 6y + 3x – 8 = 0
a = 3, b = 6. Jadi;
m1 = – a / b = – 3/6 = – ½
Syarat gradien garis yang sejajar adalah m1 = m2 = – ½
Jadi, gradien garis yang sejajar dengan garis 6y + 3x – 8 = 0 adalah m2 = – ½
4. Persamaan garis lurus yang tegak lurus
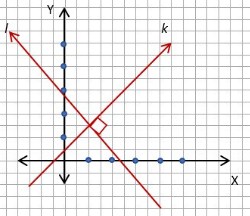
Perhatikan gambar berikut!
Gambar di atas menunjukkan diagram kartesius dari dua buah garis lurus k dan l yang tegak lurus satu sama lain.
Yang perlu digarisbawahi dalam materi ini adalah bahwa gradien dari dua garis lurus yang saling tegak lurus jika dikalikan akan menghasilkan angka -1.
Dalam matematika ditulis, misalnya;
y1 = m1x + c1
dan
y2 = m2x + c2
adalah dua persamaan garis lurus yang saling tegak lurus, maka berlaku;
m1 . m2 = -1
atau dengan kata lain rumus gradien tegak lurus adalah;
m1 = -1/m2
atau
m2 = -1/m1
a. Contoh soal persamaan garis tegak lurus:
Diketahui sebuah persamaan garis lurus berikut:
2x + y – 6 = 0
Tentukan gradien garis yang tegak lurus dengan garis tersebut.
b. Penyelesaiannya:
2x + y – 6 = 0
a = 2, b = 1, c = -6
m1 = – a/b = -2/1 = -2
Gradien garis yang tegak lurus dengan gradien tersebut adalah m1 * m2 = -1
m2 = -1/m1
m2 = -1/-2
m2 = ½
Jadi, gradien garis yang tegak lurus dengan garis 2x + y – 6 = 0 adalah ½.
5. Persamaan Garis Lurus Melalui 1 Titik
Ingat, bahwa bentuk persamaan garis lurus secara umum adalah;
y = mx + c
dengan m adalah gradien atau kemiringan.
Untuk menentukan persamaannya, maka digunakan rumus persamaan garis lurus yang melalui satu titik (x1, y1);
y – y1 = m (x – x1)
a. Contoh Soal:
Tentukan persamaan garis yang melalui titik (4,3) dengan gradien sebesar 2.
b. Pembahasan:
Cara 1: Pakai rumus umum
Diketahui titiknya adalah (x1, y1) —-> (4,3), dengan demikian nilai x1 = 4 dan y1 = 3, maka langkah selanjutnya adalah substitusi nilai m dan nilai (x1, y1) ke dalam rumus;
- y – y1 = m (x – x1)
- y – 3 = 2 (x – 4)
- y – 3 = 2x – 8
- y = 2x – 8 + 3 (pindah ruas, negatif menjadi positif)
- y = 2x – 5
Jadi, persamaannya adalah y = 2x – 5
Cara 2: pakai rumus cara cepat
Mencari nilai c dari persamaan umum garis lurus, yakni;
- y = mx + c
Substitusi nilai gradien 2 dan nilai (4, 3) ke dalam persamaan di atas;
- 3 = 2. 4 + c
- 3 = 8 + c
- c = 3 – 8
- c = – 5
Kemudian, dimasukkan atau disubstitusikan ke persamaan umum garis lurus, menjadi;
- y = mx + c
- y = 2x – 5
Jadi, persamaannya adalah y = 2x – 5
6. Persamaan Garis Lurus Melalui 2 Titik
Rumus persamaan garis melalui 2 titik (x1, y1) dan (x2, y2) adalah:
a. Contoh soal:
Tentukan persamaan garis lurus yang melalui dua titik (2, -4) dan (1, 4)!
b. Jawaban:
Diketahui x1 = 2, y1 = -4, x2 = 1, y2 = 4
Jadi, persamaan garisnya adalah y = -8x + 12
7. Contoh soal persamaan garis lurus dan jawabannya
Berikut adalah beberapa contoh soal yang bisa teman-teman pakai belajar di rumah:
a. Contoh Soal 1
Carilah persamaan garis yang sejajar dengan persamaan garis lurus y = 2x – 3 dan melalui titik (4,3).
Jawaban dan penyelesaian:
Diketahui, persamaan garis lurus pertama adalah y = 2x – 3
Di mana y1 = m1x + c1 maka y = 2x – 3, yang artinya m1= 2.
Karena garisnya sejajar, maka m1 = m2 = 2.
Substitusikan nilai m2 = 2 di atas pada persamaan y = mx + c. Substitusikan juga nilai x dan y yang dilalui oleh garis tersebut.
- y = mx + c
- 3 = 2.4 + c
- 3 = 8 + c
- c = 3 – 8
- c = -5
Dengan demikian, dapat disimpulkan bahwa persamaan garis lurus yang sejajar dengan garis y = 2x – 3 adalah y = 2x – 5.
b. Contoh Soal 2
Tentukan persamaan garis lurus yang sejajar dengan garis 2x + 3y + 6 = 0 dan melalui titik (-2, 5)!
Jawaban dan penyelesaian:
Langkah pertama, ubah dulu persamaan 2x + 3y + 6 = 0 dalam bentuk persamaan umum, menjadi;
- 2x + 3y + 6 = 0
- 3y = -2x – 6
- y = -2/3 x – 2
Dengan begini, nilai m1 = -2/3
Atau cari nilai m1 memakai rumus m1 = -a/b dari persamaan:
- 2x + 3y + 6 = 0 —> ax + by + c = 0
- m1 = -2/3
Kemudian, m1 = m2 = -2/3 (karena sejajar), substitusikan pada persamaan berikut titik yang dilalui oleh garis tersebut;
- y = mx + c
- 5 = -2/3 . -2 + c
- 5 = 4/3 + c
- c = 5 – 4/3
- c = 11/3
Substitusi ke persamaan umum lagi;
- y = mx + c
- y = -2/3x + 11/3 (dikalikan 3 semua)
- 3y = -2x + 11
- 2x + 3y – 11 = 0
Jadi, persamaan garis yang sejajar dengan 2x + 3y + 6 = 0 adalah 2x + 3y – 11 = 0.
c. Contoh Soal 3
Tentukan persamaan garis lurus yang tegak lurus dengan garis y – 2x + 3 = 0 dan melalui titik (4,3)!
Jawaban dan penyelesaian:
Kita perlu mengubah dulu persamaannya dalam bentuk umum y = mx + c, yakni;
- y – 2x + 3 = 0
- y = 2x – 3
Dari persamaan ini, dapat diketahui bahwa gradien garisnya adalah 2, ditulis m1 = 2.
Atau kita bisa mencari nilai m1 dari rumus -a/b.
Persamaannya adalah y – 2x + 3 = 0 —-> ax + by + c = 0
Sehingga :
- a = -2, b = 1, dan c = 3.
- m1 = -a/b = – (-2/1) = 2
Karena tegak lurus, maka m1 . m2 = -1 atau m2 = – ½
Selanjutnya, teman-teman bisa menyubstitusi nilai m2 yang sudah diperoleh dan koordinat titik (4,3) ke dalam persamaan y = mx + c menjadi;
- 3 = – ½ .4 + c
- c = 3 + 2
- c = 5
Persamaan kedua dapat dicari dengan cara substitusi;
- y = mx + c
- y = – ½ x + 5
Jadi, persamaan garis lurus yang tegak lurus terhadap garis y = 2x – 3 adalah
- y = – ½ x + 5.
d. Contoh Soal 4
Sejajar atau tegak luruskah garis y – 3x + 4 = 0 dan y – 3x – 2 = 0?
Jawaban dan penyelesaian:
Persamaan 1;
- y – 3x + 4 = 0
- y = 3x – 4
- m1 = 3
Persamaan 2;
- y – 3x – 2 = 0
- y = 3x + 2
- m2 = 3
Jadi, dua garis tersebut sejajar, karena m1 = m2 = 3
e. Contoh Soal 5
Sejajar ataukah tegak lurus persamaan garis lurus 3x – y = 5 dan –x – 3y = 6 ?
Jawaban dan penyelesaian:
Persamaan pertama;
- 3x – y = 5
- -y = -3x + 5 (kalikan dengan -1)
- y = 3x – 5
- m1 = 3
Persamaan kedua;
- –x – 3y = 6
- -3y = x + 6
- y = (x + 6)/-3
- y = – 1/3 x – 2
- m2 = -1/3
Kemudian, cari hubungan antara m1 dan m2, sebagai berikut;
- m1 . m2 = 3 . (-1/3) = -1
Dengan demikian, kedua garis ini tegak lurus.
f. Contoh Soal 6
Tentukan persamaan garis lurus yang tegak lurus dengan garis 2x + 3y + 6 = 0 dan melalui titik (-2, 5)!
Jawaban dan penyelesaian:
2x + 3y + 6 = 0, maka
- a = 2, b = 3, c = 6
- m1 = -a/b = -2/3
Karena tegak lurus, maka:
- m2 = -1/m1 = 3/2
Persamaan garis yang melalui titik (-2, 5) adalah…
- y – y1 = m (x – x1)
- y – 5 = 3/2 [x – (-2)]
- y = 3/2 x + 3 + 5
- y = 3/2 x + 8 (semua dikali 2)
- 2y = 3x + 16
- 3x – 2y + 16 = 0
Jadi, garis yang tegak lurus dengan garis 2x + 3y + 6 = 0 dan melalui titik (-2,5) adalah 3x – 2y + 16 = 0.
8. Cara mencari titik koordinat untuk menggambar grafik diagram kartesius
Agar makin mudah memahami materi persamaan garis lurus, kak Hinda akan menggunakan soal nomor 6 di atas untuk menggambarkan contoh soal koordinat kartesius dalam bentuk diagram. Tapi sebelumnya, kita harus menentukan titik koordinatnya terlebih dulu. Berikut adalah cara mencari titik koordinat kartesius:
Pertama-tama, cari dulu koordinat (x, 0), dan (y,0)
- Persamaan 1: 2x + 3y + 6 = 0
- Untuk nilai y = 0, maka nilai x adalah:
- 2x + 0 + 6 = 0
- 2x = -6
- x = -3
- Untuk nilai x = 0, maka nilai y adalah:
- 0 + 3y + 6 = 0
- 3y = -6
- y = -2
Kemudian ambil 2 titik lain sembarang
- Misal x = -1 dan x = 1 maka jika dimasukkan ke dalam persamaan ditemukan secara berturut-turut y = -4/3 dan y = -8/3.
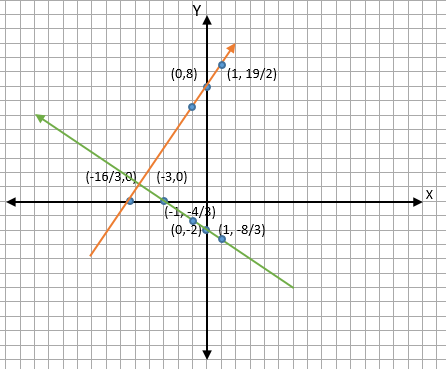
Sehingga kita mendapatkan 4 koordinat, yakni: (0, -2), (1, -8/3), (-1, -4/3), dan (-3, 0). Hubungkan keempat titik dalam diagram kartesius.
Persamaan: 2x + 3y + 6 = 0 | |
x | y |
0 | -2 |
1 | -8/3 |
-1 | -4/3 |
-3 | 0 |
Lakukan hal serupa untuk persamaan kedua. Maka akan ditemukan 4 titik koordinat sebagai berikut:
(0, 8), (1, 19/2), (-1, 13/2), dan (-16/3, 0)
Hubungkan keempat titik koordinat tersebut dalam diagram kartesius sehingga terbentuk sebuah garis lurus.
Persamaan: 3x – 2y + 16 = 0 | |
x | y |
0 | 8 |
1 | 19/2 |
-1 | 13/2 |
-16/3 | 0 |
Jadi, jika digambar dalam diagram kartesius hasilnya:
Catatan:
Dalam membuat diagram kartesius, langkah paling penting dan mudah adalah dengan mencari nilai titik koordinat kartesius (x, 0) dan atau (y, 0) terlebih dulu. Dengan langkah ini, maka akan jauh lebih mudah menggambarnya.
Seperti yang saya gambar di atas.
Atau jika memang sudah tahu titik yang dilalui, maka gunakan titik ini untuk membuat garis.
Demikian informasi tentang gradien persamaan garis lurus, dua garis yang sejajar, tegak lurus, dan garis yang melalui satu titik. Juga, bagaimana cara identifikasi apakah dua garis saling sejajar atau tegak lurus.
Selamat belajar.






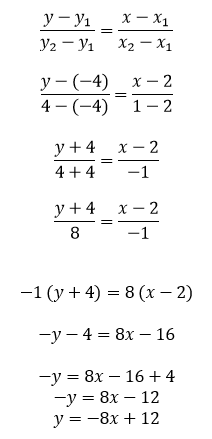
terima kasih, sangat bermanfaat ^_^
Sama-sama, alhamdulillah kalau bermanfaat
ane masih bingung
Mungkin bisa diperjelas, bingungnya dibagian mana?
terimaksih bermanfaat bgt mbak 🙂
terimakasih tetapi belum paham bak
mksh, tapi gak ngerti…hehe:p
Bagus kok jadi agak faham
makasih banyak….saya paham….V:
Bagaimana jika ada garis yang sejajar dan tegak lurus maka persamaan garisnya bagaimana