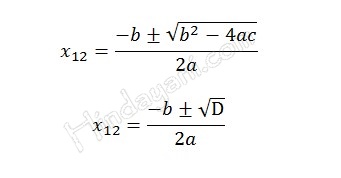Pemakaian diskriminan dalam persamaan kuadrat – Sebagaimana diketahui, mencari diskriminan bisa dilakukan untuk membantu penyelesaian soal tentang akar-akar persamaan kuadrat. Lebih khusus lagi jika Anda menyelesaikan soal persamaan kuadrat dengan rumus abc. Dalam hal ini, diskriminan berada di bawah akar kuadrat (dalam rumus abu). Karena berada di bawah akar kuadrat, maka berlaku beberapa hal tentang diskriminan berkenaan dengan penyelesaian akar persamaan kuadrat. Lebih jauh, kita akan membahasnya dalam artikel ini. Silakan disimak.
Berikut pemakaian diskriminan dalam persamaan kuadrat dan pencarian akar persamaan kuadrat
Rumus diskriminan
D = b2 – 4ac
D adalah diskriminan
Sedangkan b, a, dan c berasal dari bentuk umum persamaan kuadrat, yakni;
ax2 + bx + c = 0
Rumus abc
Rumus abc secara umum adalah;
Ketentuan Diskriminan
Dengan rumus abc di atas, maka berlaku ketentuan tentang D atau diskriminan di bawah ini;
Ketentuan pertama
Jika D > 0, maka akar-akar persamaan kuadrat merupakan bilangan riil dan tidak sama. Di sini berarti x1 tidak sama dengan x2
Ketentuan kedua
Jika D < 0 atau nilai D negatif, maka akar-akar persamaan kuadratnya adalah imaginer
Ketentuan ketiga
Jika D = 0, maka akar-akarnya merupakan bilangan riil dan nilainya sama.
Ketentuan keempat
Jika D = k2, maka akar-akar persamaan kuadratnya adalah bilangan rasional. k kuadrat adalah bilangan kuadrat seperti 16, 25, dlsb.
Baca Juga: Penyelesaian persamaan linier 3 peubah dengan metode eliminasi – substitusi
Demikian informasi tentang pemakaian diskriminan dalam persamaan kuadrat berikut ketentuannya yang harus dipahami. Semoga bermanfaat.
Selamat belajar – hindayani.com