Pemfaktoran bentuk aljabar dan persamaan kuadrat merupakan salah satu materi yang sering sekali keluar di ujian. Materi ini diajarkan dari kelas 7 8 9 SMP / MTs hingga SMA / MA / SMK kelas 10 11 12.
Maka dari itu, kak Hinda merasa materi ini penting untuk dibahas di situs ini. Supaya teman-teman yang belum paham bisa mengikuti materi cara memfaktorkan aljabar dengan riang.
Kak Hinda akan membahas secara bertahap ya? Karena kita akan mengupas contoh soal faktorisasi aljabar dan penyelesaiannya secara menyeluruh. Jadi harus pelan-pelan dan bertahap. Siap?
- Daftar Isi tampilkan
Cara pemfaktoran bentuk aljabar, rumus abc, contoh soal dan jawaban (kelas 7-12)
Sebelum kak Hinda membahas lebih jauh mengenai pemfaktoran bentuk aljabar. Yuk kita ingat dulu seperti apa pemfaktoran itu.
Teman-teman tentu sudah pernah mengerjakan soal seperti ini:
- Faktor dari 12 adalah …
Ketika ada pertanyaan itu maka jawabannya adalah:
- 1 x 12
- 2 x 6
- 3 x 4
Itulah faktor-faktor dari 12.
Pemfaktoran aljabar kurang lebih juga sama dengan pemfaktoran di atas. Bedanya adalah ada variabelnya, ada suku-sukunya.
Pemfaktoran aljabar bentuk sederhana
Untuk mendapatkan faktorisasi bentuk aljabar sederhana, kita biasanya menggunakan cara ‘mengeluarkan koefisien yang sama’. Agar lebih jelas silakan simak beberapa contoh berikut ini:
- Faktorkanlah ay + by = …
Apakah yang sama dari persamaan di atas? Yups, yang sama adalah y, jadi bisa dikerjakan dengan cara:
ay + by = y (a + b)
- Faktorkanlah 5p + 5q = …
Yang sama adalah 5, jadi faktor aljabar:
5p + 5q= 5 (p+q)
- Faktorkanlah 6a – 6b = …
Yang sama adalah 6, jadi:
6a – 6b = 6 (a – b)
- Faktorkanlah 2x + 2y =…
Yang sama adalah 2, jadi:
2x + 2y = 2 (x + y)
- Faktorkanlah 3x + 6y =
Maka teman-teman bisa mengerjakannya dengan cara berikut:
3x + 6y = 3x + (3.2) y = 3 (x + 2y)
Langkah untuk mengerjakan contoh kelima:
- Cari dulu faktor dari 6, yaitu 1 x 6 dan 2 x 3.
- Pilih salah satu faktor yang sama koefisiennya dengan variabel x, yaitu 3. Keluarkan.
Dengan beberapa contoh di atas, kita bisa menyimpulkan bahwa pemfaktoran bentuk aljabar sederhana satu atau dua suku bisa diselesaikan memakai cara ‘mengeluarkan koefisien yang sama’.
Dari contoh di atas pula ada pola yang bisa kita lihat, yaitu sebuah bentuk umum berikut:
ax + bx = x (a + b)
Untuk lebih mendalami tentang aljabar, kak hinda sudah menuliskan contoh soal aljabar secara lengkap tentang perkalian, pembagian, penjumlahan, dan pengurangan.
Pemfaktoran persamaan kuadrat
Selanjutnya, kak hinda akan mengajak teman-teman untuk membahas pemfaktoran pada persamaan kuadrat. Yang mana, materi ini sering sekali muncul di soal ujian.
Ada beberapa cara yang bisa dilakukan untuk mendapatkan faktor dari fungsi kuadrat, di antaranya adalah:
a. Cara silang
Dalam penyelesaian faktorisasi menggunakan cara silang, teman-teman bisa mengikuti langkah di bawah ini:
- Cari nilai a dalam bentuk umum ax2 + bx + c
- Cari faktor dari a
- Cari faktor dari c
- Lakukan perkalian silang yang jika dijumlahkan mendapatkan b
Contoh soal pemfaktoran cara silang:
Tentukan faktor dari: x2 – 5x + 4
Jawaban:
dari contoh di atas, a = 1, b = -5, dan c = 4
Faktor dari 1 (a) adalah [1 x 1], [-1 x -1]
Faktor dari 4 (c) adalah, [1 x 4], [2 x 2], [-1 x -4], [-2 x -2]
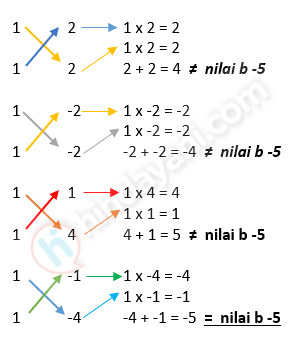
Kemudian kita hitung perkalian silang antara faktor (a) dan (b) untuk dicocokkan hasilnya dengan (b):
Karena sudah ada nilai yang sama dengan nilai b = -1, maka sudah diketahui berapa faktor dari 4 yang akan dipakai. Yakni -1 dan -4.
Jadi, faktor dari fungsi kuadrat di atas adalah:
x2 – 5x + 4 = (x – 1) (x – 4)
b. Rumus ABC pemfaktoran
Teman-teman bisa menggunakan rumus pemfaktoran di bawah ini untuk mencari nilai x1 dan x2 kemudian dimasukkan dalam bentuk pemfaktorannya. Rumus ini biasa disebut rumus abc.
Ini rumusnya:
Dengan hasil faktornya adalah:
ax2 + bx + c = (x – x1) (x – x2)
Contoh soal rumus abc:
Tentukan faktor dari x2 – 5x + 4
Jawab:
Dari soal di atas, kita tahu a = 1, b = -5, c = 4
Maka jawaban dari contoh soal persamaan kuadrat dan penyelesaiannya menggunakan rumus abc di atas adalah:
Kemudian dimasukkan ke dalam rumus abc pemfaktoran berikut:
x2 – 5x + 4 = (x – x1) (x – x2) = (x – 4) (x – 1)
c. Rumus pemfaktoran lainnya
Apakah teman-teman ingat rumus ini?
x2 – y2 = (x + y) (x – y)
Rumus di atas juga dikenal dengan rumus selisih dua kuadrat. Teman-teman bisa menggunakan rumus ini sebagai cara memfaktorkan persamaan kuadrat. Tapi tidak semua bentuk fungsi kuadrat bisa diselesaikan pakai rumus ini.
Contoh soal pemfaktoran persamaan kuadrat dan penyelesaiannya dengan rumus ini adalah:
- x2 – 25 = (x – 5) (x + 5)
- x2 – 64 = (x + 8) (x – 8)
Teman-teman bisa lihat bahwa bilangan 25 dan 64 merupakan bilangan kuadratik atau bisa diakar kuadratkan dengan sempurna.
Jadi, ketika teman-teman menemui soal seperti:
- x2 – 27
- x2 – 81
Manakah yang bisa diselesaikan memakai rumus selisih dua kuadrat?
Yups, tentu yang x2 – 81. Sebab 81 bisa diakarkan menjadi 9.
Hasilnya adalah x2 – 81 = (x – 9) (x + 9)
Contoh soal persamaan kuadrat dengan cara memfaktorkan:
- Faktorkan 2x2 – 18y2 = …
Penyelesaian:
- 2x2 – 18y2 = 2x2 – (2.9) y2 —-> Keluarkan angka 2
- 2x2 – (2.9) y2 = 2 (x2 – 9y2) —-> ingat 9 = 32 dan 9y2 = (3y)2
- 2 (x2 – 9y2) = 2 (x + 3y) (x – 3y)
Jadi, faktor dari 2x2 – 18y2 = 2 (x + 3y) (x – 3y)
d. Pakai cara cepat
Cara cepat memfaktorkan sangat umum dipakai untuk menyelesaikan soal pemfaktoran persamaan dan fungsi kuadrat hingga mencari himpunan penyelesaiannya.
Langkah memfaktorkan fungsi kuadrat dengan cara cepat:
- Kalikan dulu nilai a dengan c (termasuk tanda positif dan negatifnya). Misal a . c = d
- Temukan dua angka yang jika dikalikan dapat angka d dan jika dijumlahkan dapat b
Cara ini tergolong mudah dan cepat.
Contoh Soal:
6x2 – 19 x + 15 = …
Pembahasan:
- Cari dua angka yang jika dikalikan dapat nilai 90 dan jika dijumlahkan dapat nilai -19. Angka tersebut adalah -9 dan -10.
- Ingat bahwa nilai a adalah 6, maka bentuknya menjadi;
- (2x ….) (3x…..)
- Sehingga jika dikalikan nanti mendapatkan 6x2. Kemudian Anda bisa memasukkan angka -9 dan -10. Catatannya, pilih angka yang bisa dibagi 3, yakni -9 (dibagi 3 menjadi -3) dan letakkan di dalam kurung yang jauh dari angka 3x, menjadi;
- (2x – 3) (3x …)
- Kemudian pilih angka yang bisa dibagi 2, yakni -10 (dibagi 2 menjadi -5) dan letakkan di dalam kurung yang jauh dari 2x, menjadi;
- (2x – 3 ) ( 3x – 5 )
- Jadi, hasil dari pemfaktoran 6x2 – 19 x + 15 = (2x – 3 ) ( 3x – 5 )
e. Memanfaatkan bentuk (x-a)2 atau (x + a)2
Selain cara-cara di atas, teman-teman juga bisa menyelesaikan persamaan dengan menyempurnakan bentuk kuadratnya.
Misalnya:
x2 – 6x + 8 = …
Penyelesaian:
- x2 – 6x + 8 = …
- x2 – 6x = -8
- x2 – 6x + 9 = -8 + 9
- (x – 3)2 = 1
- x – 3 = -1 atau x – 3 = 1
- x = 2 atau x = 4
Jadi, jika ditulis dalam bentuk faktor hasilnya:
- x2 – 6x + 8 = (x – 2) (x – 4)
f. Rangkuman bentuk faktor sebagai bahan persiapan olimpiade
Jika teman-teman mengikuti lomba olimpiade Matematika, maka mengetahui rangkuman rumus pemfaktoran sangatlah penting.
Dari formula yang paling sederhana hingga yang rumit. Berikut adalah beberapa di antaranya:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b + c)2 = a2 + b2 + c2 + 2(ab + ac + bc)
- a2 – b2 = (a + b) (a – b)
- (a + b)3 = a3 + b3 + 3ab (a + b)
- (a – b)3 = a3 – b3 – 3ab (a – b)
- (a + b)3 = (a + b)(a2 – ab + b2)
- (a – b)3 = (a – b)(a2 + ab + b2)
- (a + b)(a – b)2 = a3 – a2b – ab2 + b3
- a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – ac – bc)
- (a + 1)(b + 1)(c + 1) = abc + ab + ac + bc + a + b + c + 1
- a4 + 4b4 = (a2 + 2ab + 2b2 )(a2 – 2ab + 2b2 )
- (a + b)4 = a4 + b4 + 4ab(a2 + b2 ) + 6a2 b2
- (a – b)4 = a4 + b4 – 4ab(a2 + b2 ) + 6a2 b2
Sedangkan untuk bentuk ke-n pemfaktoran dan penjabaran bisa dibaca di bawah ini:
- an + bn = (a + b) (an-1 – an-2b + an-3b2 – … – abn-2 + bn-1) untuk n anggota bilangan ganjil.
- an – bn = (a – b) (an-1 + an-2b + an-3b2 + … + abn-2 + bn-1) untuk n anggota bilangan genap.
Contoh soal dan penyelesaian
Soal-soal di bawah ini mohon untuk dikerjakan dahulu. Baru kemudian silakan Anda koreksi jawabannya dengan melihat pembahasan yang ada di bawah.
a. Latihan soal!
- Faktorkan:
- x2 – 6x + 5 =
- 2x2 + 7x + 6 =
- x2 – 16 =
- 2r2 – 8s2 =
- 5pq + 3pr =
- Diketahui sebuah persamaan kuadrat x2 – 2x – 8 = 0. Tentukan 3x + y jika y = 4.
- Panjang dari sebuah persegi panjang bernilai x cm. Nilai x-nya sendiri bisa dicari dari fungsi kuadrat berikut:
x2 – 4x + 3 = 0, dengan syarat x > 1 cm
Jika lebar persegi panjang tersebut adalah y = 15 cm. Berapakah keliling persegi panjangnya.
b. Penyelesaian!
- Berikut adalah penyelesaian soal di atas:
- x2 – 6x + 5 = (x – 1) (x – 5)
- a = 1, b = -6, c = 5
- a x c = 1 * 5 = 5.
- Bilangan yang jika dikalikan dapat 5 dan dijumlahkan dapat -6 adalah -1 dan -5.
- Jadi, x2 – 6x + 5 = (x – 1) (x – 5)
- 2x2 + 7x + 6 =
- a = 2, b = 7, c = 6
- a*c = 2 * 6= 12,
- Bilangan yang jika dikalikan hasilnya 12 dan dijumlahkan hasilnya 7 adalah 3 dan 4. Maka faktor dari 2x2 + 7x + 6 adalah:
- 2x2 + 7x + 6 = (2x + 3) (x + 2)
- x2 – 16 = (x + 4) (x – 4) ——> (bentuk akar kuadrat sempurna)
- 2r2 – 8s2 = 2 (r2 – 4s2) = 2 (r + 2s) (r + 2s)
- 5pq + 3pr = p (5q + 3r)
- x2 – 2x – 8 = 0
- (x – 4) (x + 2) =0
- x – 4 = 0 atau x + 2 = 0
- x = 4 atau x = -2
- 3x + y = 3.4 + 4 = 16 atau 3x + y = 3. (-2) + 4 = -2
- x2 – 4x + 3 = 0
- (x – 1) (x – 3) = 0
- x = 1 atau x = 3
- Syaratnya adalah x > 1, maka nilai x yang digunakan adalah 3.
- Jadi, keliling persegi panjangnya adalah:
- 2 (p + l) = 2 (x + y) = 2 ( 3 + 15) = 2 . 18 = 36 cm
Trik menyederhanakan persamaan kuadrat berbentuk pecahan
Selain soal seperti di atas, biasanya contoh soal pemfaktoran juga dibuat seperti pecahan. Kemudian kita diminta untuk menyederhanakannya.
Untuk mengerjakan soal semacam ini, kak Hinda punya tipsnya:
a. Terbiasa memfaktorkan
Karena kita ingin membuat bentuk sederhana dari dua persamaan dan fungsi kuadrat, maka kita harus bisa memfaktorkan dulu. Agar bisa cepat, kita harus sering berlatih mengerjakan soal pemfaktoran. Juga mengenali beberapa trik cepat pemfaktoran.
Saya sudah pernah membuat videonya di youtube, berikut linknya:
Dalam video di atas saya memakai contoh yang sederhana. Namun, jika sering dilatih, maka kemampuan pemfaktoran akan menjadi lebih bagus.
b. Selalu ada faktor yang sama
Antara dua fungsi kuadrat yang difaktorkan, pembilang dan penyebut. Pasti ada satu faktor keduanya yang sama.
Sebab faktor inilah yang nantinya bisa dibagi atau biasa kita sebut dicoret sehingga tinggal faktor lainnya dalam bentuk paling sederhana.
c. Mencari faktor bilangan
Dalam cara cepat memfaktorkan, kita harus mencari dua bilangan yang jika dikalikan hasilnya adalah perkalian a dengan c (fungsi kuadrat ax^2 + bx + c). Dan dua bilangan tersebut jika dijumlahkan hasilnya adalah b.
Nah, dari sini apa yang harus kita siapkan?
Kita harus tahu bagaimana mendapatkan dua angka itu dengan cepat. Yakni dengan cara mencari faktor bilangan (perkalian antara a dengan c). Baru setelah ketemu faktor bilangan tersebut, kita bisa mencari mana yang jika dijumlahkan hasilnya menjadi b.
Nah, sudah jelas, agar bisa memfaktorkan persamaan kuadrat dengan cepat, kita juga harus terbiasa mencari faktor bilangan dengan cepat.
d. Teliti
Yang paling sering terjadi adalah salah meletakkan tanda positif dan negatif. Biasanya kesalahan ini terjadi saat memfaktorkan. Biasanya tanda dari b tidak begitu diperhatikan sehingga salah dalam memilih faktor bilangan yang hendak dimasukkan ke dalam faktor persamaan kuadrat.
Ini fatal.
Sebab jika terjadi bisa menyebabkan kesalahan pada pengerjaan soal hingga selesai. Bahkan, kamu mungkin tidak akan bisa menemukan bentuk sederhana karena tidak ada faktor sama yang dapat dicoret.
e. Sering berlatih
Lantas, bagaimana mengatasinya?
Mudah saja, kamu harus sering berlatih memfaktorkan fungsi kuadrat. Perbanyaklah latihan soal. Kenali apa saja bagian yang harus kamu pahami. Mana yang masih terasa sulit buatmu, dan mana yang sudah kamu kuasai.
Mengenali kelemahanmu sendiri merupakan kunci untuk memperbaiki diri.
Itulah beberapa trik menyederhanakan persamaan kuadrat yang selama ini saya aplikasikan. Jika penjelasan di atas kurang bisa dipahami, silakan tonton video berikut untuk pembelajaran secara audiovisual.
Itulah materi pemfaktoran bentuk aljabar sederhana satu hingga dua suku dan pemfaktoran persamaan kuadrat. Semoga bermanfaat.



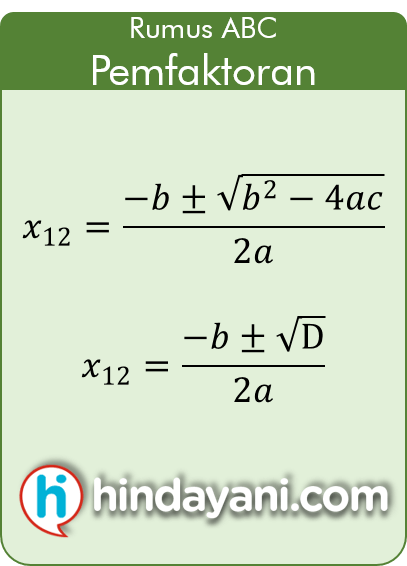

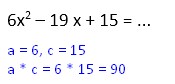


sip
Aku suka cara cepatnya kak