Persamaan linear merupakan salah satu materi aljabar yang diajarkan di SMP/MTs hingga SMA/MA/SMK.
Di bangku kuliah pun materi ini masih diajarkan. Yakni dalam mata kuliah Aljabar Linear Elementer.
Dalam kesempatan kali ini, kak Hinda membatasi pembahasan persamaan linier hanya untuk tingkat sekolah saja.
Sebuah persamaan linear biasanya digambarkan dengan garis lurus dalam diagram kartesius. Maka dalam Matematika biasanya kita mengenal gradien, ukuran kemiringan dari garis lurus tersebut.
Namun, dalam pembahasan kali ini kak Hinda akan fokus pada sistem persamaan linear (SPL) dan metode penyelesaiannya saja.
Kita akan membahas SPL satu variabel, dua variabel, tiga variabel dengan masing-masing metode penyelesaiannya.
Seperti elimininasi, substitusi, dan matriks (pakai determinan). Agar lebih jelas, teman-teman bisa langsung membacanya dalam pembahasan berikut.
Catat dulu bahwa kak Hinda akan membuat tulisan ini secara bertahap sesuai tingkat kesulitannya. Sebab materi ini biasanya diajarkan di tingkat SMP MTs hingga SMA MA SMK.
Sistem persamaan linear – 2 dan 3 variabel (metode penyelesaian dan contoh)
Mengutip dari wikipedia, pengertian persamaan linear adalah sebuah persamaan aljabar. Yang mana tiap sukunya mengandung konstanta. Atau merupakan perkalian konstanta dengan variabel tunggal.
Lalu, bagaimana dengan sistem persamaan linear?
Mari kita kenali dulu apa itu sistem persamaan linear.
Sistem Persamaan Linear
Pengertian SPL adalah persamaan linear yang dikorelasikan hingga membentuk sebuah sistem.
Sistem persamaan linear bisa mengandung satu, dua, tiga variabel, atau lebih.
Kak Hinda akan lebih banyak membahas tentang sistem persamaan linear dua variabel (SPLDV) dan sistem persamaan linear tiga variabel (SPLTV) berikut langkah menyelesaikan persamaannya.
Namun, kakak akan tetap mengulas materi sistem persamaan linear satu variabel (SPLSV) dalam artikel ini. Materi ini biasanya diajarkan di bangku kelas 7 SMP MTs. Silakan disimak ya teman-teman.
Dengan pembahasan SPLSV, kak Hinda harap teman-teman juga bisa memahami materi lanjutannya dengan cepat.
Jangan khawatir, materi ini tidak serumit namanya kok. Memang cukup panjang sampai harus disingkat namanya. Hihihi.
Sistem Persamaan Linear Satu Variabel (SPLSV)
Pengertian SPLSV
Nah, SPLSV adalah sebuah kalimat terbuka yang tanda hubungnya adalah sama dengan (‘=’). SPLSV juga hanya memiliki satu variabel yang berpangkat 1.
SPLSV ada kaitannya dengan kalimat terbuka, lho! Jadi kalau teman-teman belum paham materi tentang kalimat terbuka, silakan buka tulisan saya tentang kalimat terbuka berikut:
https://hindayani.com/logika-matematika-pernyataan-dan-kalimat-terbuka/
Bentuk umum SPLSV
Bentuk umum dari SPLSV adalah:
- ax + b = c
Dengan a, b, dan c adalah anggota bilangan bulat tak nol.
Contoh SPLSV
Diketahui sebuah persamaan berikut:
- 2x – 3 = 7
Berapakah x = ?
Jawaban:
- 2x – 3 = 7
- 2x = 7 + 3 –> 3 pindah ruas, sebelumnya pengurangan (negatif) jadi penjumlahan (positif)
- 2x = 10
- x = 10 : 2 –> 2 pindah ruas, sebelumnya perkalian, jadi pembagi
- x = 5
Selain contoh dalam bentuk persamaan ringkas seperti di atas, soal SPLSV biasanya juga dalam bentuk soal cerita dalam kehidupan sehari-hari.
Misalnya:
Bonbon berangkat membeli kaca persegi sebanyak 4 buah dan 1 ban. Dia sempat membaca label bahwa harga ban 4000. Dan dia harus membayar total belanjanya senilai 52000.
Pada saat kembali ke rumah, Tayo bertanya pada Bonbon harga kacanya. Dia pun menghitungnya menggunakan cara sistem persamaan linear satu variabel.
Jawaban:
Dengan kalimat dalam soal cerita di atas bisa kita buat kalimat terbukanya:
4 kaca persegi + 4000 = 52000
Jika harga kaca persegi dimisalkan x, maka kalimat di atas menjadi:
4x + 4000 = 52000
4x = 52000 – 4000
4x = 48000
x = 48000 / 4
x = 12000
Jadi, harga satu kaca persegi adalah 12000.
Sistem Persamaan Linear Dua Variabel (SPLDV)
Setelah paham mengenai SPLSV, sekarang kita belajar ke yang lebih luas, yaitu SPLDV. Biasanya materi ini dijelaskan di kelas 8 SMP.
Sesuai dengan namanya, SPLDV ini memiliki dua variabel. Biasanya ditulis x dan y, p dan q, dll. Agar lebih jelas, silakan simak!
Pengertian SPLDV
SPLDV adalah sebuah sistem persamaan linear yang terdiri dari dua persamaan. Di mana dua persamaan itu memiliki masing-masing dua variabel.
Sistem persamaan linear dua variabel biasanya menggunakan variabel x dan y, atau p dan q, atau variabel lainnya.
Namun, yang paling umum digunakan adalah x dan y.
Ciri-ciri SPLDV
Dari pengertian di atas, ciri-ciri SPLDV adalah:
- Persamaannya memiliki dua variabel
- Menggunakan tanda sama dengan (=)
- Kedua variabel yang ada dalam persamaan berpangkat atau berderajat satu
Bentuk umum SPLDV
ax + by = p
cx + dy = q
dengan a, b, c, d, p, dan q adalah bilangan real.
- Jika p, q = 0, maka persamaan di atas disebut persamaan homogen.
- Jika p, q tidak sama dengan 0, maka persamaan di atas disebut persamaan tak homogen.
Berikut adalah contoh persamaan homogen dan tak homogen.
- Persamaan homogen
- 2x + 7y = 0
- 4x + 6y = 0
- Persamaan tak homogen
- x + 3y = 9
- 5x – y = 12
Istilah penting
Dalam SPLDV (sistem persamaan linear dua variabel) ada beberapa istilah yang perlu teman-teman tahu yaitu Suku, Variabel, Koefisien, dan Konstanta.
- Suku
Yakni bagian dari bentuk aljabar yang terdiri dari konstanta, variabel, dan koefisien.
Setiap suku dipisahkan pakai operasi penjumlahan dan pengurangan.
Contoh:
5x + 6y + 18
Maka suku-sukunya adalah:
5x, 6y, dan 18
- Variabel
Yaitu peubah atau pengganti dari suatu bilangan. Biasanya dilambangkan atau ditulis dalam bentuk huruf kecil x dan y. Atau bisa huruf lain seperti a dan b, p dan q.
Contoh:
Devya memiliki 4 boneka barbie dan 3 boneka beruang.
Pernyataan di atas jika ditulis dalam bentuk persamaan menjadi:
– Boneka barbie = x
– Boneka beruang = y
– Persamaannya akan menjadi 4x + 3y
- Koefisien
Yaitu suatu bilangan yang merupakan banyaknya jumlah variabel sejenis. Simpelnya, kak Hinda memahami koefisien sebagai bilangan yang ada di depan variabel.
Contoh:
Diketahui sebuah persamaan 4x + 3y. Dari persamaan tersebut koefisiennya adalah 4 dan 3.
4 adalah koefisien dari x.
3 adalah koefisien dari y.
- Konstanta
Nilai konstanta selalu konstan (tetap), yaitu suatu bilangan yang tidak diikuti oleh variabel. Berdiri sendiri. Nilainya tetap untuk variabel atau peubah berapa-pun.
Misalnya:
Diketahui sebuah persamaan linear dua peubah
2x + 6y – 14
Konstanta dalam persamaan di atas adalah -14.
Metode penyelesaian
Biasanya, dalam menyelesaikan soal persamaan linier 2 variabel, teman-teman akan diminta menjawab soal-soal jenis berikut;
- Mencari nilai x atau y atau keduanya (mencari nilai variabelnya)
- Mencari satu nilai dari persamaan yang di dalamnya terkandung x dan atau y.
Sistem persamaan linear dua variabel bisa diselesaikan dengan beberapa cara yaitu Substitusi, Eliminasi, Kombinasi dan Determinan.
Metode Substitusi SPLDV
Pengertian metode substitusi adalah sebuah cara yang digunakan untuk menyelesaikan persamaan linear dengan ‘memasukkan’ salah satu persamaan ke dalam persamaan lainnya.
- Tips dan langkah metode subtitusi
Berikut adalah langkah-langkah memakai metode substitusi dalam menyelesaikan soal SPLDV:
- Ubah salah satu persamaan menjadi x = f (y) atau y = f(x)
Artinya, ubah salah satu persamaan dalam bentuk fungsi lainnya.
Misal; 2x + y = 1. Maka ubahlah menjadi y = 1 – 2x atau x = (1-y) /2
Agar mudah, akan lebih baik jika teman-teman memilih yang paling mudah bentuknya. Dalam hal ini disarankan untuk memilih y = 1 – 2x saja.
- Lalu Substitusikan
Langkah kedua, teman-teman harus menyubstitusikan persamaan yang didapat ke persamaan lainnya. Dalam hal ini, dibutuhkan 2 persamaan linier dengan 2 peubah sekaligus.
- Contoh dan pembahasan 1
2x + y = 5 (sebut sebagai persamaan 1) dan
3x – 2y = 4 (sebut sebagai persamaan 2)
- Lakukan langkah pertama, ubah persamaan
Dari persamaan 1 didapatkan persamaan di bawah ini;
y = 5 – 2x (sebut persamaan 3)
Substitusilah persamaan di atas ke dalam persamaan kedua.
- Lalu substitusikan
3x – 2y = 4 menjadi;
3x – 2 . (5 – 2x) = 4
3x – 10 + 4x = 4 (kumpulkan koefisien bervariabel x, disusul konstanta dengan konstanta)
3x + 4x = 4 + 10
7 x = 14
x = 14/7
x = 2
Langkah selanjutnya, teman-teman bisa memasukkan kembali nilai x yang teman-teman dapatkan dalam persamaan 1 yang telah diubah yakni persamaan 3;
y = 5 – 2x
y = 5 – 2 . 2
y = 5 – 4
y = 1
Dari soal di atas, sudah diketahui bahwa himpunan penyelesaian persamaan x,y adalah 2,1 atau biasa ditulis;
Hp= {(2,1)}
- Contoh soal dan pembahasan 2
Silakan perhatikan contoh soal di bawah ini agar lebih jelas:
Tentukan nilai x dan y dari persamaan berikut ini!
x + 3y = 7
2x + 3y = 5
Jawaban:
Pada metode substitusi, langkah pengerjaannya adalah;
- Salah satu persamaan harus diubah menjadi x = atau y =
- Masukkan persamaan yang sudah diubah itu ke persamaan lainnya.
Mari kita mulai dengan langkah 1, dibentuk menjadi x =
x + 3y = 7
x = 7 – 3y
Persamaan keduanya adalah;
2x + 3y = 5, substitusikan nilai x di atas ke persamaan tersebut, menjadi;
2 (7 – 3y) + 3y = 5
14 – 6y + 3y = 5
14 – 3y = 5
-3y = 5 – 14
-3y = -9
y = 3
Sekarang nilai y sudah ditemukan, teman-teman bisa mensubstitusikan kembali nilai y ke dalam persamaan x = 7 – 3y, menjadi;
x = 7 – 3y
x = 7 – (3.3)
x = 7 – 9
x = -2
Jadi, Hp = {x, y} = {-2,3}
Metode Eliminasi SPLDV
Salah satu cara yang umum digunakan untuk menyelesaikan soal SPLDV selain substitusi adalah eliminasi. pengertian eliminasi adalah sebuah metode yang bisa digunakan untuk menyelesaikan soal SPLDV dengan ‘menghilangkan’ atau mengeliminasi satu variabel yang nilai koefisiennya sama. Kalau nilai koefisiennya belum sama, ya disamakan dulu.
- Langkah-langkah
Berikut adalah langkah-langkah untuk mengerjakan SPLDV dengan metode eliminasi:
- Eliminasi variabel x
- Eliminasi variabel y
Note: boleh dibolak-balik, pastikan cari yang mudah dulu.
Agar mudah, berikut contoh dan pembahasan disertai langkahnya:
- Contoh dan Penyelesaian 1
Tentukan himpunan penyelesaian dari persamaan berikut ini;
2x + y = 5
3x – 2y = 4
Jawaban:
Eliminasi variabel x
Eliminasi variabel x dapat dilakukan dengan cara menyamakan koefisien variabel x, yakni;
2x + y = 5 | x3
3x – 2y = 4 | x2 menjadi;
6x + 3y = 15
6x – 4y = 8
Jika koefisien x sama-sama positif atau sama-sama negatif, maka eliminasi dengan menggunakan pengurangan. Berikut kelanjutannya;
6x + 3y = 15
6x – 4y = 8 (-)
0 + 7y = 7
7y = 7
y = 1
Eliminasi variabel y
2x + y = 5 | x2
3x – 2y = 4 | x1, hasilnya;
4x + 2y = 10
3x – 2y = 4
Karena koefisien y bertanda positif dan negatif (berbeda), maka untuk mengeliminasi digunakan penjumlahan. Hasilnya;
4x + 2y = 10
3x – 2y = 4 (+)
7x + 0 = 14
7x = 14
x = 14/7
x = 2
Jadi, himpunan penyelesaian dari persamaan linier di atas adalah 2,1 atau ditulis;
Hp = { (2,1) }
- Contoh soal dan pembahasan 2
Tentukan nilai x dan y atau himpunan penyelesaian dari:
x + 3y = 7
2x + 3y = 5
- Jawaban:
Perhatikan nilai koefisien y dari persamaan pertama dan kedua, sama-sama 3. Maka untuk menghilangkan atau mengeliminasinya, operasi hitung yang digunakan adalah – (pengurangan) >> biar menjadi 0.
x + 3y = 7
2x + 3y = 5 (-)
-x = 2
x = -2
kemudian untuk mencari nilai y, teman-teman bisa melakukan eliminasi juga. Yang disamakan
x + 3y = 7 | x2
2x + 3y = 5 | x1, hasilnya;
2x+ 6y = 14
2x + 3y = 5 (-)
0 + 3y = 9
3y = 9
y = 9/3 = 3
Hp = {x, y} = {-2,3}
Sampai sini, kak Hinda harap teman-teman bisa paham metode substitusi dan eliminasi. Sebab selanjutnya kita mau bahas keduanya (kombinasi).
Metode Kombinasi (Eliminasi – Substitusi) SPLDV
Menyelesaikan sistem persamaan linear dua variabel bisa memakai cara kombinasi. Yaitu menggabungkan cara eliminasi dan substitusi.
- Langkah-langkah
- Lakukan eliminasi dengan cara menyamakan koefisien variabel (jika belum sama).
- Cari nilai salah satu variabel.
Substitusikan nilai variabel tersebut ke salah satu persamaan awal (pilih yang mudah).
Berikut adalah contoh penggunaan langkah 1 dan 2.
2x + y = 5 |x3
3x – 2y = 4 |x2
Keterangan: perkalian ini ditujukan untuk mengeliminasi variabel x, jadi nanti hasilnya tinggal variabel y. Jika teman-teman ingin mengeliminasi variabel y, maka cukup kalikan persamaan pertama dengan 2 dan persamaan kedua dengan 1.
Untuk sekarang, mari kita lakukan eliminasi variabel x.
6x + 3y = 15
6x – 4y = 8
Kurangkan dua persamaan di atas (karena tandanya koefisien x sama), menjadi;
6x + 3y = 15
6x – 4y = 8 (-)
0 + 7y = 7
7y = 7
y = 1
Berikut adalah penggunaan langkah 3
Setelah itu, teman-teman bisa memasukkan nilai y dalam salah satu persamaan (bisa persamaan 1 bisa persamaan 2). Misalnya, teman-teman memilih persamaan 1, maka hasilnya;
2x + y = 5
2x = 5 – y
2x = 5 – 1
2x = 4
x = 2
Dari sini, dapat ditarik kesimpulan bahwa himpunan penyelesaiannya adalah (2,1). Atau biasa dituliskan sebagai berikut;
Hp = {(2,1)}
- Contoh soal dan pembahasan
Berikut adalah cara menyelesaikan contoh soal yang sama dengan soal pada bagian substitusi menggunakan cara kombinasi:
Tentukan nilai x dan y atau himpunan penyelesaian dari x + 3y = 7 dengan 2x + 3y = 5!
Jawaban!
Perhatikan nilai koefisien y dari persamaan pertama dan kedua, sama-sama 3. Maka untuk menghilangkan atau mengeliminasinya, operasi hitung yang digunakan adalah – (pengurangan) >> biar menjadi 0.
x + 3y = 7
2x + 3y = 5 (-)
-x = 2
x = -2
Ketika nilai x sudah teman-teman ketahui, teman-teman bisa mencari nilai y dengan memasukkan (substitusi) nilai x tersebut ke salah satu persamaan. Misal teman-teman masukkan ke persamaan pertama, x + 3y = 7.
3y = 7 – x
3y = 7 – (-2)
3y = 9
y = 9/3 = 3
Hp = {-2,3}
Catatan:
Berikut adalah catatan dan kesimpulan pemakaian cara eliminasi dan substitusi dalam SPLDV:
- Untuk substitusi, usahakan memilih persamaan yang mudah ketika menentukan x = … atau y = …
- Untuk eliminasi, biasanya kesulitannya dalam menentukan tanda pengurang atau penjumlah saat ingin menghilangkan (eliminasi) salah satu variabel. Jadi teman-teman bisa melakukan cara di bawah ini;
- Cari koefisien yang nilainya sama
- Jika nilai yang sama itu sama-sama positif atau sama-sama negatif maka operasi hitungnya adalah pengurangan atau negatif
- Sebaliknya, jika tandanya berbeda, satu positif satu negatif, maka operasi hitungnya adalah penjumlahan atau positif.
- Kalau pakai cara kombinasi, baiknya pada saat melakukan eliminasi. Eliminasilah variabel yang nilai koefisiennya kecil. Agar angka akhirnya tidak terlalu besar saat dikalikan. Atau langsung cari yang koefisiennya sama.
- Kemudian substitusikan ke persamaan yang paling sederhana dan mudah dihitung.
Selanjutnya kakak akan mengajak teman-teman untuk mencari penyelesaian SPLDV menggunakan determinan.
Metode Determinan SPLDV
Penyelesaian SPLDV menggunakan determinan berhubungan erat dengan konsep matriks.
Untuk memahaminya secara sederhana berikut kak Hinda sudah merangkum beberapa langkah dalam mengerjakan sistem persamaan linear dua peubah menggunakan determinan:
- Langkah
- Temukan / cari determinannya.
- Tentukan nilai variabel dari determinan yang telah didapatkan sebelumnya.
Agar lebih paham silakan simak ulasannya secara lengkap.
- Rumus
Misalnya diketahui dua persamaan linear dua peubah adalah sebagai berikut;
- Contoh
Sekarang, mari kita pahami penyelesaian persamaan linier dengan 2 peubah dengan metode determinan ini menggunakan contoh.
Misalkan;
Persamaan pertama: 2x + y = 5,
persamaan kedua: 3x – 2y = 4.
Maka tentukanlah himpunan penyelesaiannya dengan metode determinan.
Jawaban!
Berikut adalah langkah menyelesaikan SPLDV pakai determinan.
Langkah 1
Langkah 2
Selanjutnya, teman-teman bisa menentukan nilai x dan y
x = det x / det
= -14/-7
= 2
y = det y / det
= -7/-7
= 1
Himpunan penyelesaian
Dari paparan di atas, dapat ditemukan nilai x dan y adalah 2 dan 1. Atau dituliskan Hp = {(2,1)}
Sistem Persamaan Linear Tiga Variabel (SPLTV)
Setelah SPLSV dan SPLDV, sekarang saatnya kita belajar SPLTV. Biasanya materi ini diajarkan di tingkat SMA, MA, SMK.
Bahkan masih berlanjut di bangku kuliah. Khususnya materi Aljabar Elementer.
Pengertian SPLTV
SPLTV diartikan sebagai sebuah konsep atau metode yang dipakai untuk menyelesaikan soal persamaan linear yang tidak bisa diselesaikan menggunakan SPLDV dan SPLSV.
SPLTV juga diartikan sebagai sebuah sistem persamaan linear yang mengandung 3 variabel dan 3 persamaan linear.
Ciri-ciri SPLTV
Jadi, syarat atau ciri SPLTV bisa dikerjakan adalah ada 3 variabel (misalnya x, y, z) dan 3 persamaan yang mengandung 3 variabel tersebut. Selain itu, SPLTV juga pasti menggunakan tanda sama dengan (=).
Bentuk umum SPLTV
Berikut adalah bentuk umum sistem persamaan linear tiga variabel:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
dengan a1, a2, a3, b1, b2, b3, c1, c2, c3, d1, d2, dan d3 adalah bilangan real.
Istilah penting
- Suku
Yakni bagian dari bentuk aljabar yang terdiri dari konstanta, variabel, dan koefisien.
Setiap suku dipisahkan pakai operasi penjumlahan dan pengurangan.
Contoh:
5x + 6y – 2z + 18
Maka suku-sukunya adalah:
5x, 6y, -2z, dan 18
- Variabel
Yaitu peubah atau pengganti dari suatu bilangan. Biasanya dilambangkan atau ditulis dalam bentuk huruf kecil x, y, dan z. Atau bisa huruf lain seperti p, q, dan r.
Contoh:
Devya memiliki 4 boneka barbie, 3 boneka beruang, dan 1 boneka kelinci.
Pernyataan di atas jika ditulis dalam bentuk persamaan menjadi:
Boneka barbie = x
Boneka beruang = y
Boneka kelinci = z
Persamaannya akan menjadi 4x + 3y + z
- Koefisien
Yaitu suatu bilangan yang merupakan banyaknya jumlah variabel sejenis. Simpelnya, kak Hinda memahami koefisien sebagai bilangan yang ada di depan variabel.
Contoh:
Diketahui sebuah persamaan 4x + 3y + z. Dari persamaan tersebut koefisiennya adalah 4, 3, dan 1.
4 adalah koefisien dari x.
3 adalah koefisien dari y.
1 adalah koefisien dari z.
- Konstanta
Nilai konstanta selalu konstan (tetap), yaitu suatu bilangan yang tidak diikuti oleh variabel. Berdiri sendiri. Nilainya tetap untuk variabel atau peubah berapa-pun.
Misalnya:
Diketahui sebuah persamaan linear tiga peubah
2x + 6y – z – 16
Konstanta dalam persamaan di atas adalah -16.
Metode penyelesaian Eliminasi SPLTV
Langkah-langkahnya adalah:
- Eliminasi pada persamaan 1 dan 2
- Eliminasi pada persamaan 1 dan 3
- Eliminasi pada persamaan yang didapatkan pada langkah 1 dan 2
- Substitusi
Contoh:
Agar lebih mudah memahami persamaan linier 3 peubah dengan metode eliminasi, berikut contoh soal yang akan kita kerjakan bersama. Carilah nilai x, y, dan z dari persamaan berikut ini.
x + y – 2z = 3 …….. (pers 1)
2x – 3y + z = 6 ….. (pers 2)
2x – 2y –z = 8 ……. (pers 3)
Pembahasan:
Langkah 1
Kita hendak membuat SPLTV di atas menjadi SPLDV. Sehingga harus ada 1 variabel yang dihilangkan.
Gunakan metode eliminasi untuk menemukan persamaan dua peubah antara persamaan 1 dan 2, caranya;
x + y – 2z = 3 | x1
2x – 3y + z = 6 | x2, dari persamaan ini didapatkan;
x + y – 2z = 3
4x – 6y + 2z = 12 (+) (mengeliminasi variabel z, tanda berbeda maka dijumlahkan)
5x – 5y = 15 (sebut persamaan 4)
Langkah 2
Lakukan metode eliminasi pada persamaan 1 dan 3 untuk mendapatkan persamaan linear dengan 2 variabel.
x + y – 2z = 3 | x1
2x – 2y – z = 8 | x2, didapatkan;
x + y – 2z = 3
4x – 4y – 2z = 16 (-) (Karena tanda koefisien z sama-sama negatif, maka dikurang)
-3x + 5y = -13 atau 3x – 5y = 13 (dikali -1) (sebut persamaan 5)
Keterangan: saat melakukan eliminasi pada langkah 1 dan 2, pastikan bahwa yang dieliminasi adalah variabel yang sama. Misal z dengan z, atau x dengan x, atau y dengan y.
Langkah 3
Sekarang kita sudah mendapatkan persamaan linier 2 peubah atau variabel yaitu persamaan 4 dan 5. Selanjutnya akan kita eliminasi:
5x – 5y = 15
3x – 5y = 13 (-) (eliminasi variabel y, tanda sudah sama-sama negatif sehingga dikurangi)
2x – 0 = 2
2x = 2
x = 1
Langkah 4
Selanjutnya, kita akan mengeliminasi x, untuk menemukan y:
5x – 5y = 15 |x3
3x – 5y = 13 |x5
15x – 15x = 45
15x – 25y = 65 (-)
0 + 10y = -20
10y = -20
y = -2
Langkah 5
Untuk mengetahui nilai z, kita bisa langsung melakukan substitusi nilai x dan y ke dalam persamaan:
x + y – 2z = 3
1 + (-2) – 2z = 3
-1 – 2z = 3
– 2z = 3 + 1
-2z = 4
z = 4 : (-2)
z = -2
Dengan demikian, didapatkan nilai x = 1, nilai y = -2, dan niai z = -2. Jadi, himpunan penyelesaiannya adalah
Hp= {1, -2, -2}
Cara ini tergolong cara cepat, karena mengombinasikan eliminasi dan substitusi di akhir. Jika kita melakukan eliminasi full. Setelah langkah 4 bisa ditemukan persamaan 6 dan 7 bervariabel y atau z (misalnya).
Metode Penyelesaian Substitusi SPLTV
Untuk mengerjakan soal SPLTV dengan metode substitusi ada beberapa langkah:
- Ubah salah satu persamaan menjadi x =, y =, atau z = (Sebut persamaan 4)
- Substitusi persamaan 4 ke dua persamaan lain (misal persamaan 2 dan 3)
- Kerjakan soal persamaan dua variabel baru yang diperoleh dengan cara substitusi hingga selesai.
Agar mudah memahaminya, silakan simak contoh di bawah ini:
Contoh
Kita akan mencoba mengerjakan soal di atas menggunakan metode substitusi:
x + y – 2z = 3
2x – 3y + z = 6
2x – 2y –z = 8
Pembahasan
x + y – 2z = 3 ……….. (pers 1)
2x – 3y + z = 6 …….. (pers 2)
2x – 2y –z = 8 ………. (pers 3)
Langkah 1
x + y – 2z = 3
x = 3 – y + 2z ………. (pers 4)
Langkah 2
Substitusi persamaan 4 ke persamaan 2:
2x – 3y + z = 6
2 (3 – y + 2z) – 3y + z = 6
6 – 2y + 4z – 3y + z = 6
-5y + 5z = 0 ………… (pers 5)
Langkah 3
Sekarang, substitusikan persamaan 4 ke persamaan 3:
2x – 2y – z = 8
2 (3 – y + 2z) – 2y – z = 8
6 – 2y + 4z -2y – z = 8
-4y + 3z = 2 ……….. (pers 6)
Langkah 4
Kita akan mengerjakan persamaan 5 dan 6.
Dari persamaan 5, kita peroleh:
5z = 5y
z = y
Kemudian kita substitusi ke persamaan 6, menjadi:
-4y + 3z = 2
-4z + 3z = 2
-z = 2
z = -2
y = z = -2
Langkah 7
Kemudian kita akan mencari nilai x dengan mensubstitusikan nilai y dan z ke dalam persamaan 4:
x = 3 – y + 2z
x = 3 – (-2) + 2. (-2)
x = 3 + 2 – 4
x = 1
Jadi, nilai x, y, dan z berturut-turut adalah 1, -2, dan -2.
Himpunan penyelesaian persamaan di atas adalah {1, -2, -2}
Metode penyelesaian Determinan SPLTV
Seperti halnya saat mengerjakan soal SPLDV menggunakan SPLTV, determinan sangat erat kaitannya dengan matriks. Jadi, sebelumnya mari kita ubah bentuk umum SPLTV menjadi bentuk matriks.
- Bentuk umum
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
Jika dibentuk dalam matriks menjadi:
- Rumus umum determinan matriks 3×3
Determinan (D) dirumuskan:
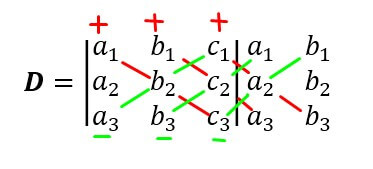
Kalau teman-teman bingung bagaimana menentukan perkaliannya, silakan lihat gambar berikut:
Selain mencari nilai D, untuk menyelesaikan SPLTV dengan determinan, kita juga harus mencari nilai Dx, Dy, dan Dz.
Berikut adalah rumus untuk mencari nilai x, y, dan z:
Sekarang, mari kita langsung mengerjakan contoh soal dan membahasnya ya? Soalnya masih sama seperti di atas. Supaya benar salahnya lebih mudah dideteksi.
- Langkah
Untuk mengerjakan soal persamaan linear 3 variabel menggunakan determinan, silakan ikuti langkah di bawah ini:
- Ubah persamaannya ke dalam bentuk matriks.
- Cari nilai determinannya.
- Cari nilai determinan x.
- Cari nilai determinan y.
- Cari nilai determinan z.
- Cari nilai x, y, z seperti rumus.
Contoh
Cari nilai x, y, dan z menggunakan determinan!
x + y – 2z = 3
2x – 3y + z = 6
2x – 2y –z = 8
Pembahasan
Berikut langkah-langkah yang bisa teman-teman ikuti:
Langkah 1
Mari kita ubah dalam bentuk matriks dulu:
Langkah 2
Cari determinannya:
D = 3 + 2 + 8 – 12 + 2 + 2
D = 5
Langkah 3
Determinan x
Dx = 9 + 8 + 24 – 48 + 6 + 6
Dx = 5
Langkah 4
Determinan y
Dy = -6 + 6 – 32 + 24 – 8 + 6
Dy = -10
Langkah 5
Determinan z
Dz = -24 + 12 – 12 + 18 + 12 – 16
Dz = -10
Langkah 6
Mencari nilai x, y, dan z:
x = 5 : 5 = 1
y = -10 : 5 = -2
Z = -10 : 5 = -2
Jadi, nilai x, y, dan z berturut-turut adalah 1, -2, dan -2.
Kumpulan contoh soal dan pembahasan
Contoh soal 1 – SPLDV Substitusi
Tentukan nilai x dan y dari persamaan berikut;
y = -8x + 3
4x + 5y = 6
Jawaban!
Jika kita lihat secara sekilas, contoh soal di atas bisa diselesaikan dengan metode substitusi, karena ada unsur y = . Maka kita akan coba menyelesaikannya dengan metode substitusi dengan memasukkan nilai y = -8x + 3 ke dalam persamaan kedua, menjadi;
4x + 5.(-8x + 3) = 6
4x -40x + 15 = 6
-36 x = 6 – 15
-36x = -9
x = ¼
kemudian, untuk mendapatkan nilai y, mari kita masukkan nilai x dalam persamaan pertama, y = -8x + 3, menjadi;
y = -8 . ¼ + 3
y = -2 + 3
y = 1
Jadi, himpunan penyelesaiannya adalah ¼, 1 atau Hp = { ¼, 1}
Anda bisa mencoba menggunakan metode eliminasi jika mau.
Contoh soal 2 – SPLDV Eliminasi
Mari kita coba cari himpunan penyelesaian dari sistem persamaan linier 2 variabel di bawah ini dengan metode eliminasi, sebab koefisien dari variabel y nya bisa dihilangkan secara langsung.
-3x – 2y = 6
5x – 2y = -26 (-)
-8x = 32
x = -4
kemudian, masukkan nilai x ke salah satu persamaan, misalnya -3x – 2y = 6, maka akan menjadi;
-2y = 6 + 3x
-2y = 6 + 3. (-4)
-2y = 6 – 12
-2y = -6
y = 3
Dengan demikian, Hp = {-4,3}
Dalam bentuk soal lainnya, teman-teman diminta untuk mencari satu nilai, misalnya cari nilai 2x + 3y dari persamaan;
-3x – 2y = 6
5x – 2y = -26
Kita sudah tahu kalau nilai x dan y dari persamaan di atas adalah -4 dan 3, maka dari itu kita bisa langsung memasukkan nilainya ke dalam soalnya;
2x + 3y = (2. (-4)) + (3.3) = -8 + 9 = 1
Contoh soal 3 (soal pengayaan SPLDV)
Sekarang, mari kita coba selesaikan soal pengayaan persamaan linier 2 variabel, di mana soal ini sering kita temui dalam kehidupan sehari-hari. Dalam soal ini, kita bisa melihat penggunaan persamaan linier 2 variabel dalam kehidupan kita.
Harga dua baju dan satu topi adalah Rp 170.000,00. Sedangkan harga satu baju dengan tiga topi adalah Rp 185.000,00. Tentukan harga dua topi dan tiga baju.
Langkah pertama untuk mengerjakan soal di atas adalah menyederhanakan soal ke bentuk persamaan linier dengan cara mengubah kata baju menjadi x dan topi menjadi y. Hasilnya;
2x + 1.y = 170.000
2x + y = 170.000
Kemudian berlanjut ke pernyataan kedua,
1.x + 3.y = 185.000
x + 3y = 185.000
sekarang kita sudah punya 2 persamaan linier, yakni;
2x + y = 170.000
x + 3y = 185.000
kita akan cari himpunan penyelesaiannya dengan menyamakan koefisiennya dulu;
2x + y = 170.000 | x1
x + 3y = Rp 185.000 | x2
hasilnya;
2x + y = 170.000
2x + 6y = 370.000 (-)
-5y = – 200.000
y = 40.000
Substitusikan nilai y ke salah satu persamaan;
x + 3y = 185.000
x = 185.000 – 3y
x = 185.000 – (3 x 40.000)
x = 185.000 – 120.000
x = 65.000
Yang ditanyakan adalah harga dua topi dan tiga baju, ingat, topi = y dan baju = x, maka yang ditanyakan adalah;
2y + 3x = (2 x 40.000) + (3 x 65.000) = 80.000 + 195.000 = 275.000
Jadi, harga dua topi dan tiga baju adalah Rp 275.000,00.
Contoh soal 4 – SPLDV
Tentukan nilai x dan y atau himpunan penyelesaian dari x + 3y = 7 dengan 2x + 3y = 5!
Perhatikan nilai koefisien y dari persamaan pertama dan kedua, sama-sama 3. Maka untuk menghilangkan atau mengeliminasinya, operasi hitung yang digunakan adalah – (pengurangan) >> biar menjadi 0.
x + 3y = 7
2x + 3y = 5 (-)
-x = 2
x = -2
Ketika nilai x sudah Anda ketahui, Anda bisa mencari nilai y dengan memasukkan nilai x tersebut ke salah satu persamaan. Misal Anda masukkan ke persamaan pertama, x + 3y = 7.
3y = 7 – x
3y = 7 – (-2)
3y = 9
y = 9/3 = 3
Hp = {-2,3}
Contoh soal 5 – SPLDV
Contoh soal kedua ini hanya berubah tanda saja, supaya Anda lebih mudah memahami bagaimana cara menentukan operasi hitung yang akan digunakan ketika ada koefisien yang sama dalam metode eliminasi sistem persamaan linier dua variabel.
Hitunglah himpunan penyelesaian dari persamaan linier dua variabel berikut;
x – 3y = 7
2x + 3y = 5
Maka pembahasannya menjadi;
Nilai dari koefisien y dari 2 persamaan di atas sama-sama 3, hanya saja beda tanda, yakni (+) dan (-). Jadi, operasi hitung yang harus digunakan untuk menghilangkan koefisien y adalah +. Sebab -3y + 3y = 0. Sementara jika menggunakan operasi pengurangan, hasilnya tidak akan nol melainkan -3y – 3y = 6y.
Penyelesaian persamaan linier dua variabel di atas menjadi;
x – 3y = 7
2x + 3y = 5 (+)
3x = 12
X = 12/3
X = 4
Kemudian, masukkan nilai x ke salah satu persamaan untuk mendapatkan nilai y, misal ke persamaan pertama;
x – 3y = 7
-3y = 7 – x
-3y = 7 – 4
-3y = 3
y = -1
Hp = {4, -1}
Jelas sudah, dengan perbedaan tanda saja pada persamaan membuat himpunan penyelesaiannya berbeda.
Contoh soal 6 – SPLDV
Tentukan himpunan penyelesaian dari dua persamaan berikut;
2x + 3y = -5
3x – 2y = 12
Pembahasannya;
Dapat kita lihat pada persamaan, koefisien dari variabel x pada persamaan 1 dan 2 berturut-turut adalah 2 dan 3. Kemudian, koefisien dari variabel y pada persamaan 1 dan 2 berturut-turut adalah 3 dan -2. Nilainya tidak ada yang sama, bukan?
Maka dari itu, kita bisa menyamakan koefisiennya dulu dengan cara mengalikan. Taktik pertama, pilih koefisien yang mau disamakan atau akan dihilangkan. Misal, kita mau menyamakan koefisien dari variabel x. maka;
2x + 3y = -5 ( x 3)
3x – 2y = 12 ( x 2)
Persamaan pertama kita kalikan dengan 3 supaya menghasilkan 6, sedangkan persamaan kedua dikalikan 2 supaya hasilnya juga 6. Dengan demikian, nantinya koefisien dari variabel x sama-sama 6.
6x + 9y = -15
6x – 4y = 24 (-)
13y = -39
y = -3
Masukkan nilai y ke salah satu persamaan, misal ke persamaan pertama, 2x + 3y = -5, maka hasilnya;
2x = -5 – 3y
2x = -5 – (3. (-3))
2x = -5 + 9
2x = 4
x = 2
Jadi, Hp = {2, -3}
Mari kita coba memakai contoh di atas dengan metode menyamakan koefisien. Namun, kita akan menghilangkan koefisien dari variabel y, apakah hasilnya akan sama? Mari kita coba bersama.
Contoh soal 7 – SPLDV
Tentukan himpunan penyelesaian dari dua persamaan linier berikut;
2x + 3y = -5
3x – 2y = 12
Untuk menghilangkan koefisien variabel y, kita harus membuatnya menjadi;
2x + 3y = -5 (x2)
3x – 2y = 12 (x3)
Hasilnya;
4x + 6y = -10
9x – 6y = 36 (+)
13x = 26
x = 2
Kemudian, masukkan nilai x ke salah satu persamaan, misal:
2x + 3y = -5
3y = -5 – 2x
3y = -5 – (2.2)
3y = -5-4
3y = -9
y = -3
Jadi, Hp = { 2, -3}
Demikian materi tentang sistem persamaan linear satu variabel, sistem persamaan linear dua variabel, dan SPLTV. Mulai dari pengertian, langkah mengerjakan, rumus, dan contoh soal.
Silakan isi kolom komentar jika ingin berdiskusi tentang materi ini.








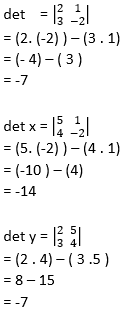

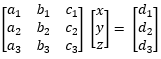
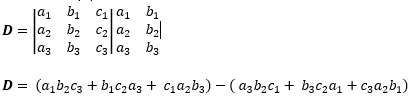

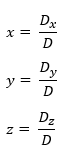
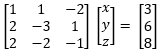
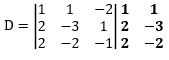
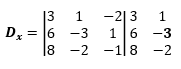
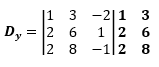
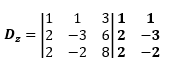
Makasih
terimakasih
hatur nuhun
thank you
terimah kasih soalnya………….