Cara Cepat Hitung Pola Bilangan Deret Angka: Rumus Contoh Soal

Materi tentang pola bilangan sangat erat kaitannya dengan barisan dan deret. Hal ini karena saat menyelesaikan soal barisan, kita perlu menentukan pola atau rumusnya terlebih dulu. Setelah ketemu rumus atau polanya maka kita akan mengerjakan soalnya dengan lebih mudah.

Jadi, materi ini biasanya diajarkan sebelum materi barisan dan deret. Materi pola dalam bilangan ini bisa dibilang sebagai dasar untuk mempelajari materi tentang barisan dan deret, baik aritmatika maupun geometri.

Yang membedakan materi pola dengan barisan dan deret adalah pada jenis, kesederhanaan, dan cara penyelesaiannya saja.

Materi ini biasanya diajarkan di kelas 7 dan 8 SMP. Penasaran? Yuk simak ulasan di bawah ini!

Pengertian pola bilangan secara umum

Pola bilangan adalah suatu susunan bilangan yang teratur yang bisa kita cari polanya.

Contoh umum bilangan berpola

Bilangan berurut yang kita kenal yaitu 1, 2, 3, 4, 5, … memiliki pola yang teratur. Ini merupakan contoh umum pola bilangan.

Saat masih SD biasanya kita akan diminta untuk mencari 2 atau 3 angka berikutnya dari urutan bilangan tersebut. Misalnya dalam soal pola bilangan kelas 1 SD kita diminta untuk mencari 3 angka setelah barisan di bawah ini:

1, 2, 3, 4, 5, ..

Maka jawabannya adalah 6, 7, 8.

Ini merupakan contoh soal yang paling sederhana dalam materi pola dalam bilangan. Ternyata, pola ini sudah kita pelajari sejak masih duduk di bangku sekolah dasar ya?

Jenis bilangan berpola

Sekarang kita akan upgrade ilmu tentang pola yang ada dalam bilangan. Ada banyak macam atau jenis contoh pola bilangan. Di antaranya adalah:

1. PB ganjil
2. PB genap
3. PB persegi
4. PB persegi panjang
5. PB segitiga
6. PB fibonacci
7. PB segitiga pascal
8. PB berpangkat
9. PB dua tingkat, dll.

Keterangan: PB adalah singkatan untuk pola bilangan.

Intinya, pola ini biasanya digunakan dalam mencari pola barisan bilangan dan pola deret bilangan secara sederhana.

Dalam kesempatan kali ini Kak Hinda akan membahas jenis-jenis pola bilangan tersebut secara ringkas disertai dengan rumus, contoh soal, dan pembahasannya.

Pola bilangan ganjil

Simak penjelasan tentang PB ganjil di bawah ini ya?

Pengertian pola barisan bilangan ganjil

Pengertian pola barisan bilangan ganjil yaitu sebuah pola yang terbentuk dari barisan bilangan ganjil. Sementara kita tahu, barisan ganjil sendiri memiliki pengertian sebagai sebuah bilangan asli yang tidak habis dibagi dengan 2.

Barisan bilangan ganjil dapat dituliskan:

• 1, 3, 5, 7, 9, 11, …

Rumus pola bilangan dari barisan bilangan ganjil

Berikut ini adalah cara mencari rumus pola bilangan dari barisan bilangan ganjil:

Rumus pola dari bilangan ganjil adalah U_n = 2n – 1 dengan suku pertamanya adalah 1.

Contoh soal pola barisan bilangan ganjil dan pembahasannya

Tentukan suku ke-10 dari pola barisan bilangan ganjil!

Pembahasan:

• Suku pertama = 1
• Suku kedua = 3
• Suku ketiga = 5
• Suku keempat = 7
• Suku kelima = 9
• Suku keenam = 11
• Suku ketujuh = 13
• Suku kedelapan = 15
• Suku kesembilan = 17
• Suku kesepuluh = 19

Untuk menemukan suku berikutnya, tambahkan suku sebelumnya dengan 2. Karena barisan bilangan ganjil merupakan pola bilangan loncat satu bilangan.

Atau teman-teman bisa langsung memasukkan ke dalam rumus = 2n – 1. Didapatkan hasil sebagai berikut:

• 2n – 1 = 2 x 10 – 1 = 19

Jadi, suku kesepuluh dari bilangan ganjil adalah 19.

Pola bilangan genap

Sekarang kita akan kenalan dengan bilangan genap dan contohnya. Kak Hinda juga akan merangkum rumus atau pola dari barisan bilangannya.

Pengertian pola barisan bilangan genap

Pola bilangan genap adalah suatu susunan bilangan yang dapat membentuk bilangan genap secara teratur. Pola dari bilangan genap biasanya juga loncat satu bilangan.

Selanjutnya, berikut ini adalah pengertian bilangan genap dan contohnya:

Bilangan genap adalah bilangan yang terdiri dari anggota bilangan cacah yang habis dibagi dengan 2.

• Contoh bilangan genap adalah: 0, 2, 4, 6, 8, …
• Contoh barisan bilangan genap adalah: 2, 4, 6, 8, …

Pola barisan genap dimulai dengan 2 karena nilai n dimulai dari 1 bukan 0.

Rumus pola bilangan dari barisan bilangan genap

Berikut adalah gambar dan rumus untuk mencari pola dari bilangan genap:

Rumus untuk mencari pola dari bilangan genap adalah U_n = 2n dengan n dimulai dari 1.

Contoh soal pola barisan bilangan genap dan pembahasannya

Tentukan suku ke-7 dari pola barisan bilangan genap berikut ini:

• 2, 4, 6, 8, …, suku ke-7

Pembahasan:

• Suku pertama = 2
• Suku kedua = 4
• Suku ketiga = 6
• Suku keempat = 8
• Suku kelima = 10
• Suku keenam = 12
• Suku ketujuh = 14

Dengan kata lain, untuk mencari suku berikutnya, kita tinggal menjumlahkan bilangan sebelumnya dengan angka 2.

Teman-teman juga bisa menghitung suku ke-7 dari barisan bilangan genap dengan menggunakan rumus 2n

• 2n = 2 x 7 = 14

Pola persegi

Sekarang mari kita lihat bagaimana pola sebuah bilangan yang membentuk persegi.

Pengertian pola persegi dari sebuah bilangan

Pola persegi adalah sebuah pola dari kumpulan bilangan yang bila digambarkan bisa membentuk persegi.

Contoh pola persegi adalah barisan 1, 4, 9, 16, …

Seperti menghitung luas persegi, untuk mendapatkan bilangan di atas, kita tinggal mengalikan jumlah bola di bagian garis mendatar dan jumlah bola di bagian garis yang menurun. Misalnya untuk suku kedua kita perlu mengalikan 2 x 2 = 4. Jadi, suku kedua pola persegi adalah 4

Rumus pola persegi

Karena barisannya adalah 1, 4, 9, 16, … kita bisa menemukan polanya adalah sebagai berikut:

Rumus pola persegi U_n = n² dengan suku pertamanya adalah 1.

Contoh soal pola persegi dan pembahasannya

Tentukan suku ke 11 dari pola persegi dari barisan bilangan berikut ini:

• 1, 4, 9, 16, …

Pembahasan:

• Teman-teman bisa menggunakan rumus pola persegi yaitu n² = 11² = 11 x 11 = 21.

Jangan lewatkan serial cara cepat lainnya : Trik cepat perkalian 5.

Pola persegi panjang

Setelah persegi, kita akan membahas tentang cara mencari pola persegi panjang:

Pengertian pola persegi panjang

Pola persegi panjang adalah suatu urutan atau susunan bilangan dengan pola tertentu yang jika digambarkan dapat membentuk persegi panjang.

Perbedaan mendasar pola persegi dan pola persegi panjang adalah pembentukan bilangan dalam sebuah gambar. Kalau pola persegi membentuk gambar persegi. Kalau pola persegi panjang jelas membentuk persegi panjang.

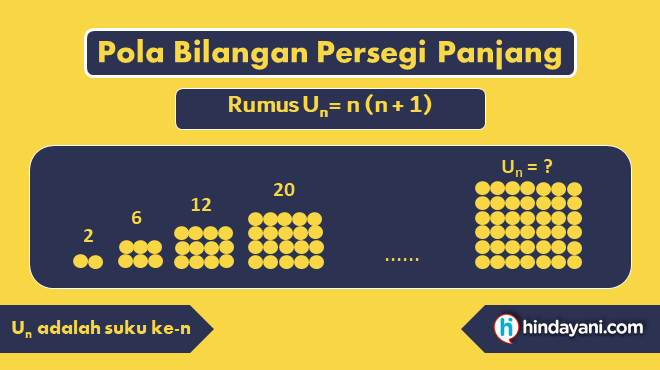
Contoh barisan bilangan dengan pola persegi panjang adalah: 2, 6, 12, 20, …

Rumus pola persegi panjang

Rumus pola bilangan yang membentuk persegi panjang adalah:

Rumus suku ke-n bilangan berpola persegi panjang adalah U_n = n (n+1) dengan suku pertamanya adalah 2.

Contoh soal pola bilangan dan jawabannya untuk pola persegi panjang

Tentukan suku ke-7 dari pola persegi panjang berikut ini:

• 2, 6, 12, 20, …

Jawaban:

• Rumus = n. (n + 1) = 7 x (7 + 1) = 7 x 8 = 56

Pola segitiga

Berikut ini adalah materi tentang pola segitiga dalam barisan bilangan:

Pengertian pola segitiga

Pola segitiga adalah sebuah susunan atau urutan bilangan dengan pola tertentu yang jika digambarkan dapat membentuk segitiga.

Bentuk umumnya adalah 1, 3, 6, 10, 15, …

Rumus pola segitiga

Silakan simak gambar dan rumus pola segitiga di bawah ini:

Dari gambar di atas kita tahu bahwa rumus suku ke-n nya adalah U_n = 0,5n (n + 1) dengan suku pertama dimulai dari 1.

Soal dan pembahasan pola bilangan segitiga

Tentukan suku ke-5 dari pola segitiga berikut ini:

• 1, 3, 6, …

Pembahasan:

• Rumus suku ke-n pola segitiga adalah 0,5n (n + 1)
• 0,5n (n + 1) = 0,5 x 5 (5 + 1) = 0,5 x 5 x 6 = 0,5 x 30 = 15

Pola fibonacci

Sudah pernah tentang barisan atau deret bilangan fibonacci? Sudah pernah tahu contoh barisan dan deret bilangan fibonacci? Ini beberapa materi dasarnya:

Pengertian pola fibonacci

Pola fibonacci adalah suatu susunan atau urutan bilangan yang setiap sukunya merupakan hasil penjumlahan dari dua suku di depannya.

Contoh bilangan fibonacci:

1, 2, 3, 5, 8, 13, 21, …

Rumus pola fibonacci

Berikut ini adalah rumus pola bilangan fibonacci: U_n = U_n-1 + U_n-2 .

Keterangan gambar:

Dua bilangan pertama dalam barisan di atas adalah 2, 4.

Suku berikutnya adalah 2 + 4 = 6, 4 + 6 = 10, 6 + 10 = 16, dan seterusnya.

Cara menghitung pola bilangan fibonacci di atas tergolong mudah. Akan tetapi pastikan teman-teman menggunakan rumus di atas setelah memastikan bahwa barisan atau deret yang dikerjakan adalah fibonacci.

Contoh pola bilangan fibonacci, soal, dan pembahasan

Berapa suku ke-6 dari barisan fibonacci berikut ini?

• 1, 3, 4, …

Pembahasan contoh soal pola bilangan di atas adalah:

Untuk mengerjakan soal di atas kita perlu mencari suku keempat dan kelima terlebih dulu dari 1, 3, 4, …

• Suku keempat = 3 + 4 = 7
• Suku kelima = 7 + 4 = 11
• Suku keenam = 11 + 7 = 18

Jadi, suku keenam barisan fibonacci di atas adalah 18.

Pola segitiga pascal

Sudah pernah dengar tentang segitiga pascal? Ya, salah satu penggunaan segitiga pascal ini adalah mencari koefisien saat menguadratkan persamaan, mencari pangkat 3 dari persamaan, hingga mencari pangkat ke-n dari persamaan.

Yuk kita simak ulasan di bawah ini agar kamu makin kenal dengan pola segitiga pascal!

Pengertian pola segitiga pascal

Pola segitiga pascal merupakan susunan atau urutan dari jumlah bilangan sebaris dalam segitiga pascal.

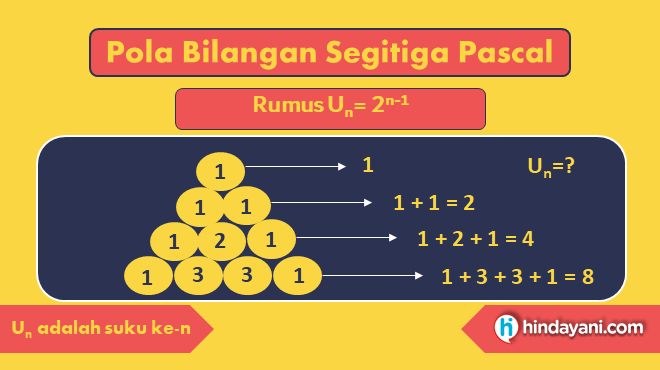
Contoh barisan segitiga pascal: 1, 2, 4, 8, 16, …

Rumus pola segitiga pascal

Berikut ini adalah rumus pola segitiga pascal:

Rumus pola segitiga pascal adalah U_n = 2^n-1 dengan n dimulai dari angka 1, suku pertama adalah 1.

Contoh soal dan pembahasan pola segitiga pascal

Tentukan suku ke 8 dari barisan segitiga pascal di bawah ini:

• 1, 2, 4, 8, 16, 32, …

Jawaban:

• Rumus = 2^n-1
• 2^n-1 = 2^8-1 = 2⁷ = 128

Jadi, suku kedelapan dari pola segitiga pascal adalah 128.

Pola bilangan berpangkat

Pada dasarnya, pola berpangkat ini hampir sama dengan pola persegi jika pangkatnya 2. Pengertian pola berpangkat adalah sebuah pola atau aturan atas barisan susunan bilangan yang terbentuk dari bentuk pangkat. Kalau pangkatnya 2, berarti kuadrat.

Contohnya adalah:

1, 4, 9, 16, …

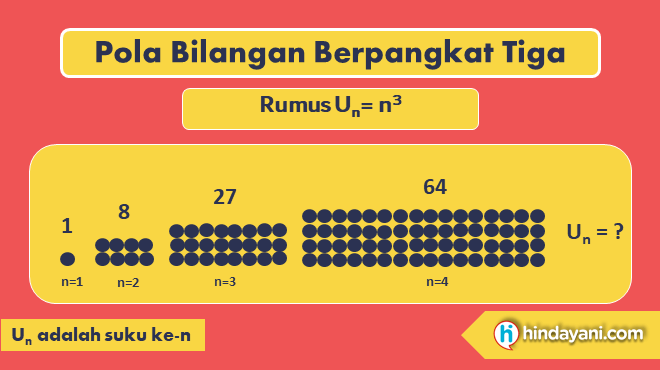
1, 8, 27, 64, …

1 merupakan bentuk kuadrat dari 1, 4 merupakan bentuk kuadrat dari 2, 9 merupakan bentuk kuadrat dari 3, 16 merupakan bentuk kuadrat dari 4, begitu seterusnya membentuk barisan secara berurutan.

Rumus pola berpangkat

Berikut ini adalah rumus pola berpangkat dua:

Rumus pola berpangkat di atas adalah U_n = n² dengan n dimulai dari 1 dan suku pertamanya adalah 1.

Berikut ini adalah rumus pola berpangkat tiga:

Rumus pola berpangkat di atas adalah U_n = n³ dengan n dimulai dari 1, dan suku pertamanya adalah 1.

Contoh soal pola berpangkat dan jawabannya

1. Tentukan nilai suku ke-9 dari barisan bilangan di bawah ini:

• • 1, 4, 9, 16, 25, …

Jawaban:

• • Rumus = n²
  • N² = 9² = 81.

Jadi, suku kesembilan dari pola berpangkat dua adalah 81.

2. Tentukan 3 bilangan selanjutnya dari pola barisan bilangan berikut ini!

• • 1, 8, 27, …

Jawaban:

Dari soal di atas jika dianalisa polanya adalah bilangan berpangkat 3. Jadi:

• • Rumusnya adalah n³

3 bilangan selanjutnya adalah suku keempat, kelima, dan keenam. Maka:

• • Suku keempat adalah 4³ = 64
  • Suku kelima adalah 5³ = 125
  • Suku keenam adalah 6³ = 216

Jadi, pola barisan bilangan di atas menjadi:

• • 1, 8, 27, 64, 125, 216

Pelajari juga trik cepat pengurangan dua bilangan kuadrat di sini.

Pola dua tingkat

Silakan simak ulasan di bawah ini untuk mengenal apa itu pola bilangan dua tingkat!

Pengertian pola dua tingkat

Pola dua tingkat didefinisikan sebagai barisan bilangan yang polanya ada dua tingkat baru terlihat sama. Agar paham, berikut adalah contohnya:

1, 4, 11, 22, 37, …

Pola dua tingkat ini biasanya menjadi soal tes potensi akademik saat hendak masuk S2 atau saat tes CPNS.

Rumus pola dua tingkat

Rumus pola dua tingkat digambarkan di bawah ini:

Rumus pola dua tingkat adalah U_n = a + (n-1) b + (n-2) c.

Penggunaan rumus di atas tergantung suku pertama dan selisih atau beda yang digunakan. Jadi, cari dulu a, b, dan c nya. Untuk rumus di atas, a = 1, b = 3, c = 4.

Contoh soal pola bilangan dan pembahasannya

Berapakah suku keenam dari pola di bawah ini:

• 1, 4, 11, 22, …

Jawaban:

• Suku pertama = 1
• Suku kedua = 4 (selisih suku kedua dan pertama adalah 3)
• Suku ketiga = 11 (selisih suku ketiga dan kedua adalah 7, merupakan hasil dari 4 + 3)
• Suku keempat = 22 (selisih suku keempat dan ketiga adalah 11, merupakan hasil dari 4 + 4 + 3)
• Suku kelima = 37 (selisih suku kelima dan keempat adalah 15, merupakan hasil dari 4 + 4 + 4 + 3)
• Suku keenam = 46 didapat dari 37 + 4 + 4 + 4 + 4 + 3 = 37 + 19 = 46.

Dari ulasan di atas bisa dilihat dengan baik polanya ya?

Cara menghitung deret angka dengan cepat tanpa rumus

Setelah belajar mengenai pola bilangan menggunakan rumus, sekarang kita akan cari tahu cara menghitung deret angka tanpa rumus. Mau tahu caranya? Silakan simak ulasan di bawah ini:

Cara menjumlahkan deret angka dengan cepat tanpa rumus

Menjumlahkan bilangan bukanlah ilmu yang bisa diremehkan meski memang gampang. Jika sekarang kamu ditantang untuk menghitung sejumlah bilangan yang berurutan dan jumlahnya lebih dari 3 atau 5, maka apa yang kira-kira akan kamu lakukan? Menggunakan kalkulator? Menggunakan rumus deret, atau yang lainnya?

Semuanya memang bisa dilakukan secara bebas. Namun, kamu bisa memilih trik cepat tanpa menggunakan kalkulator atau rumus lho. Sebagai jaga-jaga saat lupa rumusnya.

Trik ini terpakai ketika kita menjumlahkan bilangan berurut saja. Silakan simak logika, langkah serta contoh yang akan kami sajikan di bawah ini;

Logika deret hitung berurut

Perlu diketahui kalau trik ini bisa dilakukan pada deret hitung untuk bilangan berurut tanpa menggunakan rumus, menghitung satu per satu, atau bahkan menggunakan kalkulator. Hanya berlaku untuk perhitungan panjang.

Langkah penjumlahan cepat

Untuk menghitung penjumlahan yang cukup panjang, cukup gunakan bilangan terkecil dan bilangan terbesar yang ada dalam deret tersebut. Langkah-langkahnya adalah:

1. Perhatikan deret bilangan tersebut, benarkah berurutan?
2. Ambil bilangan terbesarnya kemudian bagi dengan angka 2.
3. Ambil bilangan terkecilnya lalu kurangi dengan angka 1, hasilnya bagi lagi dengan angka 2.
4. Hasil dari poin 2 dan 3 dikurangkan.
5. Jumlahkan bilangan terkecil dan terbesar, simpan hasilnya.
6. Kalikan hasil dari poin 4 dan 5.

Bingung? Jika iya, sekarang juga kita akan membahas contohnya supaya Anda jauh lebih paham lagi. Yuk simak.

Contoh soal dan pembahasan

1. Berikut adalah contoh soal dan penalaran pertama dari materi cara cepat menjumlahkan deret bilangan berurut tanpa rumus ini, simak.

Coba jumlahkan 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16

Ikuti langkah di atas;

1. • Deret berurutan
   • Bilangan terbesar adalah 16, dibagi 2, 16 : 2 = 8
   • Bilangan terkecil adalah 9, dikurangi 1, 9 – 1 = 8, kemudian dibagi 2, 8 : 2 = 4
   • Cari selisih poin 2 dan 3, 8 – 4 = 4
   • Jumlahkan bilangan terbesar dan terkecil, 9 + 16 = 25
   • Kalikan hasil poin 4 dan 5, hasilnya adalah 4 x 25 = 100

Sekarang mari kita cek contoh soal kedua ya?

2. Mari kita coba untuk menjumlahkan deret angka dengan bilangan genap sebagai bilangan terkecilnya.

8 + 9 + 10 + 11 + 12

1. • Deret berurutan
   • Angka terbesar 12 dibagi 2 = 6
   • Angka terkecil 8, dikurangi 1 = 7, kemudian dibagi 2 = 3,5
   • 6 – 3,5 = 2,5
   • 8 + 12 = 20
   • Sekarang 2,5 x 20 = 50

Sekarang, sudah cukup paham, bukan? Selamat mencoba trik cara cepat menjumlahkan deret bilangan berurut tanpa rumus ini di rumah.

Selanjutnya, bagaimana jika pola bilangan dalam deret angkanya berbeda. Misalnya disuruh menghitung deret angka dalam pola bilangan ganjil. Bagaimana caranya?

Trik Hitung Cepat Penjumlahan Deret Bilangan Pola Ganjil

Siapa yang tidak ingin bisa menghitung cepat. Dengan trik cepat, seseorang bisa menghemat banyak waktu untuk menyelesaikan satu soal Matematika.

Ini menjadi pengetahuan dasar supaya Anda bisa menyelesaikan soal Matematika dengan mudah setelah analisa dari soal tersebut. Khusus untuk kamu yang pernah menjumpai soal 1 + 3 + 5 + 7 + 9 + … + n, maka apa yang akan Anda lakukan untuk mengetahui hasilnya? Menjumlahkannya satu per satu? Menggunakan rumus deret? Atau bahkan menggunakan kalkulator?

Untuk itu, kami akan mengajak kamu menghitung deret tersebut dengan cepat tanpa menggunakan alat bantu lain selain otak dan logika berpikir yang praktis.

Dengan trik ini, saat kamu lupa kumpulan rumus deret angka, kamu tetap bisa mengerjakan soal dengan percaya diri.

Logika berpikir

Untuk menjumlahkan bilangan 1 + 3 + 5 + 7 + 9 + … + n. Kamu bisa menggunakan trik yang sederhana, yakni dengan menambahkan 1 pada bilangan terakhir yang muncul.

Lantas, membagi hasilnya dengan angka dua. Hasil akhir yang kamu dapatkan kemudian bisa dikuadratkan untuk mendapatkan hasil eksaknya. Dengan cara praktis ini, kita tidak perlu lagi;

1. Menekan tombol kalkulator secara berulang
2. Menjumlahkan secara cepat dengan mencari 2 bilangan yang bisa menghasilkan angka 10 atau 0 di belakangnya
3. Menghafal rumus, dll.

Namun yang harus menjadi perhatian adalah bahwa trik ini khusus diperuntukkan bagi deret bilangan dengan pola bilangan ganjil saja.

1, 3, 5, 7, 9, …, n

Langkah praktis penjumlahan

Berikut rahasia langkah ringkas dan trik hitung cepat penjumlahan deret bilangan pola ganjil yang bisa dilakukan;

1. Bilangan terakhir deret yang muncul ditambah dengan angka 1
2. Hasil pada poin 1 dibagi dengan angka 2
3. Hasil pada poin 2 dikuadratkan

Untuk lebih jelas lagi, Anda bisa menyimak contoh soal berikut penalarannya dan urutan langkahnya dalam sub bab di bawah ini.

Contoh soal deret angka dan pembahasannya tanpa rumus deret bilangan

A. 1 + 3 + 5 + 7 + … + 57 hasilnya adalah …

Yang Anda perlu perhatikan pertama kali adalah apakah deret tersebut adalah deret dari bilangan ganjil yang dimulai dari angka 1 atau tidak, jika deret tersebut tidak dimulai dengan angka 1, maka langkah di atas tidak terpakai.

Dan karena contoh soal deret angka di atas memakai deret dengan bilangan awal adalah angka 1, maka langkah penjumlahannya adalah;

1. Angka terakhir= 57, 57 + 1 = 58
2. 58 : 2 = 29
3. 29 x 29 = 841

Jadi, hasil dari 1 + 3 + 7 + … + 57 = 841

B. 1 + 3 + 5 + 7 + … + 23 hasilnya adalah ….

Bilangan di atas adalah merupakan bilangan pola ganjil dengan angka 1 sebagai suku pertamanya. Oleh karena itu, kamu bisa mengerjakan dengan langkah mudah;

1. Bilangan terakhir; 23 + 1 = 24
2. 24 : 2 = 12
3. 12 x 12 = 144

Jadi, hasil dari 1 + 3 + 5 + 7 + … + 23 = 144

C. 1+3+5+…+99 hasilnya adalah…

Cara menghitung deret 1 + 3 + 5 + 7 + … + 99, teman-teman bisa jadi tak perlu rumus deret bilangan. Teman-teman bisa menggunakan langkah di atas. Berikut cara menghitung deret angka dengan cepat:

1. Bilangan tersebut berpola ganjil secara berurut.
2. Bilangan terakhirnya 99. Maka 99 + 1 = 100.
3. 100 : 2 = 50
4. 50 x 50 = 2.500

Jadi, 1+3+5+7+9+…+99 hasilnya adalah 2.500.

Latihan soal

Jika kamu sudah memahami tiga contoh yang kami sajikan di atas, sekarang saatnya untuk mencoba latihan soal penjumlahan deretan angka dan bilangan di bawah ini;

1. 1 + 3 + 5 + 7 + … + 19=…
2. 1 + 3 + 5 + 7 + … + 67 = …
3. 1 + 3 + 5 + 7 + … + 55 = …

Itulah beberapa latihan soal yang bisa teman-teman coba kerjakan di rumah untuk mengasah kemampuan.

Rumus deret angka psikotes – persiapan TPA

Dari ulasan tentang rumus deret angka dan pola bilangan di atas, berikut adalah simpulan yang bisa diambil:

Hal penting sebelum mulai mengerjakan

Perhatikan dulu hal-hal di bawah ini sebelum mulai mengerjakan soal:

1. Sebelum mengerjakan soal pola bilangan maupun deret angka, pastikan dulu barisan deret bilangan tersebut. Apakah tersusun dengan pola tertentu atau tidak.
2. Jika sudah dipastikan bilangannya berpola, kerjakan sesuai pola apa yang ada dalam soal.
3. Tidak semua pola barisan bilangan tercakup dalam 9 atau 10 pola yang kami bahas di atas. Untuk itu, kita perlu mencarinya sendiri.
4. Jika mengalami kesulitan dalam mencari polanya, banyaklah berlatih.
5. Dalam cara belajar deret angka tanpa rumus, pastikan memperhatikan pola dan suku pertamanya. Sudahkah sesuai dengan kaidah atau belum.

Trik hitung cepat selalu punya kondisi-kondisi khusus, jadi memang kita harus memperhatikan syarat dan kondisi ini sebelum memulai mengerjakan soal.

Video cara mengerjakan soal deret angka psikotes tanpa rumus

Di video ini saya berbagi cara mengerjakan psikotes deret angka secara mudah. Mengenali logika dan menganalisa cara berpikirnya. Tanpa kalkulator dan cocok sekali untuk belajar TPA atau tes potensi akademik:

Demikian pembahasan tentang pola bilangan dan deret angka. Bagaimana cara mengerjakan soal tanpa rumus dengan hasil yang tepat. Semoga bermanfaat dan bila ada salah mohon dimaafkan ya! Salam.