Mean, Median, Modus merupakan salah satu ukuran pemusatan data yang sering digunakan dalam ilmu statistika. Baik itu untuk data tunggal maupun kelompok.
Materi ini sudah mulai dikenalkan di sekolah dasar, kemudian lebih detail dan jelas di SMP/MTs. Begitu juga dengan di bangku SMA/ MA/ SMK yang mengulas materi ini secara lebih rinci dengan tingkatan soal yang lebih sulit.
Dalam kesempatan kali ini, kak Hinda akan mengajak teman-teman untuk mempelajari materi ini secara bertahap dan komprehensif.
Kakak akan menuliskan materi mean, median, dan modus secara lengkap. Mulai dari pengertian, rumus, contoh, dan penyelesaiannya.
Karena nantinya materi ini akan membahas semuanya, harap teman-teman membaca sesuai kelas atau tingkatan teman-teman saat ini ya? Agar tidak bingung.
Mean, Median, Modus: Data Tunggal dan Data Kelompok (Pengertian, Rumus, Contoh, Kumpulan Soal dan Pembahasan)
Kakak akan mulai membahas dari yang paling mudah, yaitu data tunggal.
Mean Median Modus Data Tunggal
Pengertian mean, median, dan modus
Mean atau rataan adalah nilai rata-rata dari sekumpulan data yang ada. Biasanya mean juga disebut rata-rata dan dilambangkan dengan x bar.
Penggunaan istilah rata-rata mulai dikenalkan saat masih SD. Seperti saat teman-teman diminta untuk mengerjakan soal di bawah ini:
Rani, Devya, dan Najma datang ke ulang tahun Rahma. Rahma memiliki 3 roti di rumahnya untuk diberikan kepada teman-temannya tersebut. Berapakah roti yang diterima masing-masing oleh Rani, Devya, dan Najma?
Tanpa disadari, contoh soal di atas merupakan soal yang menggunakan konsep mean atau rata-rata.
Median adalah nilai tengah dari kumpulan data yang telah diurutkan dari ukuran yang terkecil.
Yang harus digaris bawahi di sini adalah ‘diurutkan’. Banyak siswa yang salah menjawab soal median karena lupa mengurutkan datanya dulu sebelum dicari nilai tengahnya.
Oleh sebab itu, kakak sarankan saat mengerjakan median. Teman-teman jangan lupa mengurutkan datanya terlebih dulu.
Setelah diurutkan ada dua ketentuan yang bisa teman-teman terapkan, yaitu:
- Data ganjil
Jika jumlah datanya ganjil, maka mediannya adalah yang terletak paling tengah.
Misalnya, jumlah datanya adalah 13, maka urutkan dulu data tersebut dari yang terkecil. Kemudian mediannya terletak di data yang berada di urutan nomor 7 (data ke-7)
- Data genap
Jika banyaknya data adalah genap, maka urutkan dulu datanya dari yang paling kecil. Kemudian cari nilai mediannya dengan mencari rata-rata dari dua data yang terletak paling tengah.
Misalnya, data berjumlah 12. Maka urutkan datanya terlebih dulu. Kemudian jumlahkan data ke-6 dan ke-7, lalu dibagi 2. Itulah nilai mediannya.
Contoh:
Diketahui sebuah data tunggal
2, 4, 6, 7, 7, 8, 9, 10. Berapakah mediannya?
Kita lihat bahwa data di atas sudah urut dari yang terkecil dan jumlah datanya adalah 8. Jadi, cara mencari mediannya adalah:
Rata-rata dari data ke-4 dan 5.
Yakni (7 + 7) : 2 = 14 : 2 = 7
Modus adalah nilai yang sering muncul dari sekumpulan data yang disajikan. Teman-teman tidak perlu mengurutkan datanya terlebih dulu saat mencari modus.
Cukup cari data yang paling sering muncul, paling banyak jumlah / frekuensinya.
Contoh:
Diketahui sebuah data tunggal
2, 4, 6, 7, 7, 8, 9, 10. Berapakah modusnya?
Modus dari data di atas adalah 7 sebab muncul 2 kali. Lebih banyak dibandingkan yang lain.
Rumus Mean Median Modus Data Tunggal
Untuk menghitung berapa mean, median, dan modus data tunggal. Berikut adalah rumus-rumusnya:
Mean
Keterangan:
- x bar adalah nilai rata-rata hitung (mean)
- x merupakan nilai data
- n merupakan banyaknya data
- f adalah frekuensi munculnya data
Median
Sebelum menggunakan rumus di bawah ini, pastikan teman-teman sudah mengurutkan datanya dari yang paling kecil.
- Jumlah data ganjil
Median terletak di data ke-
n : 2 + 1
keterangan:
n adalah jumlah data
- Jumlah data genap
Median terletak di data ke-
- n : 2 + 1, dan
- n : 2
Kemudian data tersebut dijumlahkan dibagi 2.
Modus
Untuk modus, cari yang frekuensi keluarnya paling banyak.
Contoh soal dan penyelesaian
Diketahui sebuah data:
7, 8, 9, 6, 6, 7, 8, 10, 9, 6
Tentukan mean, median, modus!
Jawaban:
- Mean = (7 + 8 + 9 + 6 + 6 + 7 + 8 + 10 + 9 + 6) : 10
- Mean = 76 : 10
- Mean = 7,6
- Median
- Untuk mencari median, urutkan dulu data dari yang terkecil:
- 6, 6, 6, 7, 7, 8, 8, 9, 9, 10
- Karena jumlah datanya genap, maka mediannya terletak di data ke:
- 10 : 2 = 5
- 10 : 2 + 1 = 6
- Data ke-5 dan ke-6 adalah 7 dan 8.
- Jadi mediannya adalah
- Median = 7 + 8 : 2
- Median = 15 : 2
- Median = 7,5
- Modus
- Untuk mencari modus, tinggal kita lihat saja mana yang paling banyak terlihat.
- 6, 6, 6, 7, 7, 8, 8, 9, 9, 10
- Nilai data yang paling sering muncul adalah 6, sebanyak 3 kali.
Baca juga materi dan soal operasi hitung aljabar yang berisi rangkuman perkalian, pengurangan, perkalian, pembagian, dan perpangkatan aljabar.
Mean Median Modus Data Kelompok
Kak Hinda akan sekali lagi memberikan gambaran tentang pengertian mean, median, modus secara ringkas. Sebab pengertiannya sebenarnya sama. Hanya beda datanya saja.
Pengertian mean median modus
Mean atau rataan adalah nilai rata-rata dari sekumpulan data yang ada. Biasanya mean juga disebut rata-rata dan dilambangkan dengan x bar.
Median adalah nilai tengah dari kumpulan data yang telah diurutkan dari ukuran yang terkecil.
Setelah diurutkan ada dua ketentuan yang bisa teman-teman terapkan, yaitu:
- Data ganjil
Jika jumlah datanya ganjil, maka mediannya adalah yang terletak paling tengah.
- Data genap
Jika banyaknya data adalah genap, maka urutkan dulu datanya dari yang paling kecil. Kemudian cari nilai mediannya dengan mencari rata-rata dari dua data yang terletak paling tengah.
Modus adalah nilai yang sering muncul dari sekumpulan data yang disajikan. Teman-teman tidak perlu mengurutkan datanya terlebih dulu saat mencari modus.
Rumus mean median modus data kelompok
Berikut adalah rumus untuk mencari mean median modus data kelompok:
Mean
Sudah dituliskan di atas bahwa rumus rata-rata untuk data dengan pengelompokan berdasarkan frekuensi kemunculannya adalah:
Keterangan:
- f merupakan frekuensi dari data
- x bar adalah mean atau rataan
- n adalah jumlah data
- x adalah nilai datanya
Lalu, bagaimana dengan data yang dikelompokkan, seperti data berikut:
| Data | frekuensi |
| 10-19 | 3 |
| 20-29 | 5 |
| 30-39 | 7 |
Nah, Sebelum kita membahas lebih jauh tentang rumus mean median modus dari data kelompok. Ada beberapa istilah yang perlu teman-teman perhatikan.
Diketahui sebuah data kelompok:
| Data | frekuensi |
| 10-19 | 3 |
| 20-29 | 5 |
| 30-39 | 7 |
| 40-49 | 2 |
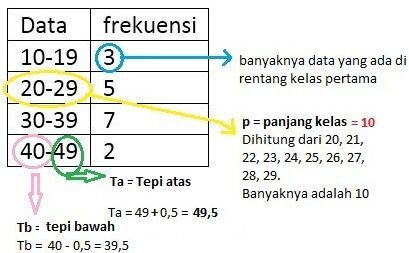
Berikut adalah istilah yang perlu teman-teman tahu sebelum kita membahas rumus median;
- Ta adalah batas atas kelas.
- Tb adalah batas bawah kelas.
- p adalah panjang kelas.
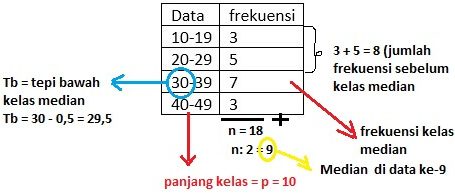
Untuk lebih jelasnya, silakan lihat gambar di bawah ini:
Keterangan: Istilah Tb, Ta, p, dan banyaknya data yang ada di rentang kelas pertama merupakan istilah penting yang erat hubungannya dengan rumus mean, median, modus dari sebuah data kelompok.
Data di atas menunjukkan data yang dikelompokkan dengan frekuensinya yang cukup besar. Rumus rata-rata atau meannya adalah:
Keterangan:
- x bar adalah rata-rata data kelompok
- fi adalah frekuensi kelas ke-i
- xi adalah nilai tengah kelas ke-i, rumusnya:
- Dengan Tb adalah batas bawah dan Ta adalah batas atas kelas
Median
Hampir sama dengan mencari nilai median dari data tunggal. Dalam data kelompok, teman-teman juga harus mencari tahu dulu letak nilai tengah dari data yang ada.
Namun, karena datanya disajikan dalam bentuk kelompok. Kumpulan data ini tidak bisa diurutkan seperti saat kita mengerjakan data tunggal.
Sehingga diperlukan sebuah rumus.
Dalam matematika kita mengenal Q1, Q2, Q3, dan Q4. Sementara untuk median ini adalah Q2, yaitu data ke-n yang membagi banyak data menjadi dua sama banyak.
Rumusnya adalah:
Keterangan:
- n adalah jumlah total frekuensi
- Tb adalah tepi bawah kelas median
- fk adalah jumlah frekuensi sebelum kelas median.
- fi adalah frekuensi kelas median
- p adalah panjang kelas
Silakan lihat gambar di bawah ini:
Berikut adalah urutan langkah mengerjakan soal median sebelum memasukkannya ke dalam rumus di atas:
- Cari berapa jumlah total frekuensinya (n)
- Bagi n dengan 2
- Hasil dari poin 2 dipakai patokan untuk menentukan dimana frekuensi kelas median yang pas. Kalau di gambar di atas, ada di data ke-9. Yakni data 30-39. Karena frekuensi sebelumnya berjumlah 8.
- Tentukan tepi bawah dari kelas median yang diketahui.
- Tentukan panjang kelas.
Modus
Mencari modus dari data kelompok agak berbeda dengan data tunggal. Dimana saat di dalam data tunggal kita cukup melihat data dengan jumlah frekuensi terbanyak.
Karena ini adalah data yang sudah dikelompokkan kita harus mencari data yang pas. Tidak menjawabnya dengan data kelompok berfrekuensi besar.
Rumus modus data kelompok adalah:
Keterangan:
- Tb adalah tepi bawah kelas modus
- Mo adalah modus
- d1 adalah selisih frekuensi kelas modus dengan frekuensi ‘sebelum’ kelas modus
- d2 adalah selisih frekuensi kelas modus dengan frekuensi ‘setelah’ kelas modus
- p adalah panjang kelas dari interval data
Silakan lihat gambar di bawah ini agar lebih jelas:
Contoh soal dan penyelesaian
Disediakan sebuah data sebagai berikut:
| Data | Frekuensi |
| 10 – 19 | 2 |
| 20 – 29 | 2 |
| 30 – 39 | 2 |
| 40 – 49 | 1 |
| 50 – 59 | 2 |
| 60 – 69 | 3 |
| 70 – 79 | 6 |
| 80 – 89 | 1 |
| 90 – 99 | 1 |
Tentukan mean, median, dan modus dari data kelompok di atas!
Penyelesaian
Mean (rataan)
Untuk mencari mean, langkahnya:
- Cari dulu xi
- x1 = (9,5 + 19,5) : 2 = 14,5
- x2 = (19,5 + 29,5) : 2 = 24,5
- x3 = (29,5 + 39,5) : 2 = 34,5
- x4 = (39,5 + 49,5) : 2 = 44,5
- x5 = (49,5 + 59,5) : 2 = 54,5
- x6 = (59,5 + 69,5) : 2 = 64,5
- x7 = (69,5 + 79,5) : 2 = 74,5
- x8 = (79,5 + 89,5) : 2 = 84,5
- x9 = (89,5 + 99,5) : 2 = 94,5
Untuk mencari nilai tengah, teman-teman sebenarnya bisa menggunakan cara berikut:
- x1 = (10 + 19) : 2 = 14,5
- x2 = (20 + 29) : 2 = 24,5
- x3 = (30 + 39) : 2 = 34,5
- x4 = (40 + 49) : 2 = 44,5
- x5 = (50 + 59) : 2 = 54,5
- x6 = (60 + 69) : 2 = 64,5
- x7 = (70 + 79) : 2 = 74,5
- x8 = (80 + 89) : 2 = 84,5
- x9 = (90 + 99) : 2 = 94,5
Jadi tak perlu mengurangkan atau menjumlahkan dengan 0,5 terlebih dulu.
Setelah tahu xi nya, silakan masukkan dalam rumus mean:
Kita harus mencari hasil kali xifi terlebih dulu:
- x1f1 = 14,5 x 2 = 29
- x2f2 = 24,5 x 2 = 49
- x3f3 = 34,5 x 2 = 69
- x4f4 = 44,5 x 1 = 44,5
- x5f5 = 54,5 x 2 = 109
- x6f6 = 64,5 x 3 = 193,5
- x7f7 = 74,5 x 6 = 447
- x8f8 = 84,5 x 1 = 84,5
- x9f9 = 94,5 x 1 = 94,5
Perhatikan tabel berikut!
| Data | Frek | xi | xifi |
| 10 – 19 | 2 | 14,5 | 29 |
| 20 – 29 | 2 | 24,5 | 49 |
| 30 – 39 | 2 | 34,5 | 69 |
| 40 – 49 | 1 | 44,5 | 44,5 |
| 50 – 59 | 2 | 54,5 | 109 |
| 60 – 69 | 3 | 64,5 | 193,5 |
| 70 – 79 | 6 | 74,5 | 447 |
| 80 – 89 | 1 | 84,5 | 84,5 |
| 90 – 99 | 1 | 94,5 | 94,5 |
Selanjutnya kita masukkan dalam rumus mean:
Jadi, mean atau rata-rata dari data kelompok di atas adalah 56.
Median
Untuk mencari median, langkahnya adalah
- n atau total frekuensi = 2 + 2 + 2 + 1 + 2 + 3 + 6 + 1 + 1 = 20
- Mediannya terletak di data ke- n : 2 = 20 : 2= 10
- Data ke- 10 ada di:
| Data | Frekuensi |
| 10 – 19 | 2 |
| 20 – 29 | 2 |
| 30 – 39 | 2 |
| 40 – 49 | 1 |
| 50 – 59 | 2 |
| 60 – 69 | 3 |
| 70 – 79 | 6 |
| 80 – 89 | 1 |
| 90 – 99 | 1 |
- Dari gambar di atas, kelas median terletak di data 60-69
- Jadi, Tb = 60 – 0,5 = 59,5
- fk = 2 + 2 + 2 + 1 + 2 = 9
- fi = 3
- p = 10
- Selanjutnya kita masukkan dalam rumus median:
Jadi, median dari data kelompok di atas adalah 62,833
Modus
Untuk mencari modus dari data kelompok, berikut adalah langkah-langkahnya:
- Cari interval data yang memiliki frekuensi terbesar.
| Data | Frekuensi |
| 10 – 19 | 2 |
| 20 – 29 | 2 |
| 30 – 39 | 2 |
| 40 – 49 | 1 |
| 50 – 59 | 2 |
| 60 – 69 | 3 |
| 70 – 79 | 6 |
| 80 – 89 | 1 |
| 90 – 99 | 1 |
Dari tabel terlihat bahwa interval data 70-79 memiliki frekuensi yang paling besar, yakni 6. Di sinilah kelas modusnya.
- Tb = 70 – 0,5 = 69,5
- d1 = 6 – 3 = 3
d2 = 6 – 1 = 5
p = 10
- Masukkan dalam rumus Mo
Jadi, nilai yang sering muncul dari data kelompok di atas adalah 73,25.
Kumpulan Soal Latihan
- Diketahui sebuah data berikut:
| Nilai | Frekuensi |
| 5 | 3 |
| 6 | 4 |
| 7 | 5 |
| 8 | 6 |
| 9 | 1 |
| 10 | 1 |
Tentukan nilai mean, median, modus!
Pembahasan:
Mean
Mean = [(5 . 3 ) + (6 . 5) + (7 . 4) + (8 . 6) + (9 . 1) + (10 . 1)] : (3 + 5 + 4 + 6 + 1 + 1)
Mean = (15 + 30 + 28 + 48 + 9 + 10) : 20
Mean = 140 / 20 = 7
Jadi, nilai mean dari data di atas adalah 7
Mencari median
Karena jumlah datanya genap, maka nilainya adalah 20/2 = 10
Jadi, jumlahkan data ke-10 dan ke-11 lalu bagi dengan 2. Yakni (7 +7) / 2 = 7
Hal ini karena 7 merupakan data ke-9, 10, 11, 12 (setelah diurutkan).
Mencari modus
Dari data di atas, sudah jelas kalau modusnya adalah nilai 8.
- Disajikan data berikut!
3, 6, 7, 9, 8, 5, 7, 8, 8, 9, 4
Penyelesaian:
Dari data di atas kita ketahui;
Banyaknya data = 11
Jika data di atas diurutkan menjadi;
3, 4, 5, 6, 7, 7, 8, 8, 8, 9, 9
Dengan begitu, maka;
Mean = [(3 x 1) + (4 x 1) + (5 x 1) + (6 x 1) + (7 x 2) + (8 x 3) + (9 x 2)] : (1 + 1 + 1 + 1 + 2 + 3 + 2)
Mean = (3 + 4 + 5 + 6 + 14 + 24 + 18) / 11
Mean = 74/11
Mean = 6,73
Mediannya adalah;
Banyaknya data ganjil, maka nilai data yang merupakan median adalah data ke; (n+1)/2 = (11 + 1)/2 = 12/2 = 6
Kemudian kita lihat, setelah diurutkan nilai data ke-6 adalah 7.
Jadi, median dari data di atas adalah 7
Modus = 8, karena muncul 3 kali. Lebih banyak dibanding dengan frekuensi nilai data lainnya.
- Disajikan data berikut!
| No | BB siswa dalam kg | Jumlah |
| 1 | 42 | 5 |
| 2 | 43 | 7 |
| 3 | 44 | 3 |
| 4 | 45 | 9 |
| 5 | 46 | 6 |
Pembahasan:
Mean
Jadi, rata-rata atau mean dari data di atas adalah 30,63.
Median
Untuk mencari mediannya;
Jumlah data = n = 30 (genap)
n : 2 = 30 : 2 = 15
Median = (nilai data ke 15 + nilai data ke 16) : 2 = (44 + 45 ) : 2 = 44,5
Jadi, median atau nilai tengah dari data di atas adalah 44,5 kg
Modus
Modus = nilai yang paling sering muncul, yakni yang jumlah siswanya terbanyak (9). Nilai datanya adalah 45 kg
Jadi, modus dari data di atas adalah 45 kg.
- Jika diketahui rata-rata nilai 9 orang siswa adalah 8,5. Jika satu siswa lagi masuk dengan nilai 7. Berapakah rata-rata nilai sekelompok siswa tersebut sekarang?
Pembahasan:
- Jumlah nilai 9 orang siswa = 8,5 x 9 = 76,5
- Jumlah nilai 10 orang siswa = 76,5 + 7 = 83,5
- Rata-rata nilai 10 orang siswa = 83,5 : 10 = 8,35
- Jika diketahui rata-rata nilai 9 orang siswa adalah x. Dan ketika satu siswa lagi masuk dengan nilai 8 rata-ratanya menjadi 6,65. Berapakah nilai x!
Jawaban
Jumlah nilai 9 orang siswa = 9x
Jumlah nilai 10 orang siswa = 9x + 8
Rata-rata nilai 10 orang siswa = (9x + 8 ) : 10 = 6,65
9x + 8 = 6,65 x 10
9x + 8 = 66,5
9x = 66,5 – 8
9x = 58,5
X = 6,5
Jadi, rata-rata nilai 9 orang siswa adalah 6,5.
Soal Latihan di Rumah
Teman-teman bisa berlatih mengerjakan soal di bawah ini untuk mempertajam kemampuan materi mean, median, dan modus data tunggal!
- Ihsan membaca novel selama seminggu dengan data di bawah ini!
Hari pertama membaca 12 halaman, hari kedua membaca 10 halaman, hari ketiga membaca 15 halaman, hari keempat membaca 10 halaman, hari kelima membaca 12 halaman, hari keenam membaca 12 halaman, hari ketujuh membaca 13 halaman.
Modus dan mean dari data di atas adalah …
- a. 10 dan 11
- b. 12 dan 13
- c. 12 dan 12
- d. 13 dan 15
- Data di bawah ini adalah data nilai Bahasa Indonesia kelas 6;
7, 6, 8, 9, 10, 8, 8, 7, 9
Rata-rata atau mean dari data di atas adalah …
- a. 7
- b. 7,5
- c. 8
- d. 8,5
- Jika dalam data di nomor 2, seorang anak dengan nilai 5 dimasukkan. Berapakah rata-ratanya …
- a. 7,2
- b. 7,5
- c. 7,7
- d. 7,9
Demikian materi mean, median, modus dari data tunggal dan data kelompok yang dapat kak Hinda sampaikan. Materi ini dikenalkan sejak SD hingga SMA. Belajarlah sesuai tingkatan teman-teman.



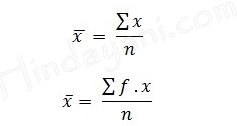
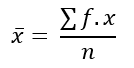
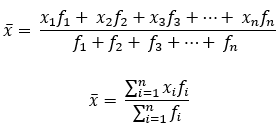
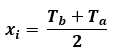
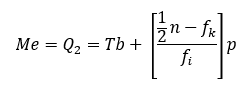
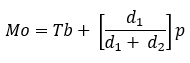

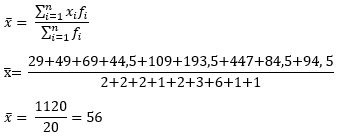

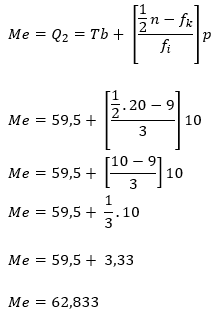
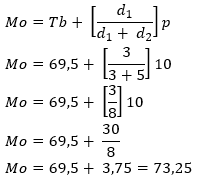
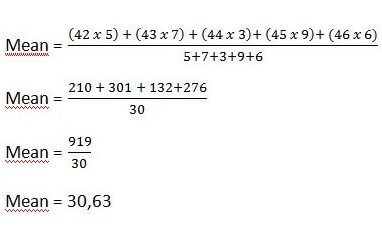
ZZZ
hahahahahaha
Hhhmmmm
keren (y)
terimakasih
matematika gk sulit kalo ada kemauan
Thank you
thnx bgt,ini sangat membantu
masa si susah aku aja dapat 100 pelajaran ini
Makasih
Lumayan lah
Thanx yoooh….
makasih 🙂
thanks ilmunya,.
mantaap
bagus
informasinya
okey mantab
tambahkan def dan soal data tunggal dan kelompok
Terima kasih atas masukannya Pak, insyaAllah. Salam kenal 🙂
terimah kasih:)
Hallo
oh gitu caranya
tapi bingung wekwekwekwekwekwekwek
Rama Rasjid Yang mana yang bingung dek?
AK AJ SUSAH PELAJARAN MATEMATIKA ASLI SUSAAAAAAH
Semangat kakak… Bisa kok asal kita rajin berlatih. Terbiasa mengerjakan soal akan menambah kemampuan kita. Percayalah…
kok gak bisa di copy yaaa..???
di disable kakak 🙂 Maaf ya, memang sengaja. Tapi semoga artikel ini tetap bisa membantu.
Thanks
You’re welcome
Sangat membantu terimakasih
Sama-sama 🙂
sangat membantu tp gak bisa d copy thu
Terima kasih 🙂 Semoga bermanfaat.
Untuk fitur copy memang sengaja di disable ya? Kalau bentuk file pdf bisa langsung diunduh.
Hai, kak Handayani..minta izin ya gimana cara mendownload contoh soal dan pengertian mean, median , dan modus ini kak trimakasih..saya ingin belajar dan ingin bisa kak..