Ada banyak jenis soal mencari besar sudut segitiga, mulai dari yang paling mudah hingga tersulit. Sayangnya, tak semua siswa bisa memahami dan mencerna cara mencari sudut segitiga dengan baik. Sehingga pada saat menemui soal, kebanyakan bingung dengan langkah dan jawaban akhirnya.
Tenang…
Dalam kesempatan kali ini kak Hinda akan memberikan cara mencari sudut pada segitiga secara sederhana. Cara-cara yang mudah dipahami dan bisa diaplikasikan saat mengerjakan soal-soal ketika ujian, seperti ulangan harian, quiz, UTS, UAS, dan UKK.
Tapi sebelum masuk ke cara mudahnya, akan lebih mudah buat teman-teman memahami apa itu sudut, apa itu segitiga, dan bagaimana cara mencari besar sudut segitiga.
Gak pakek lama! Yuk kita bahas langsung saja satu per satu.
Segitiga
Sebelum kita bahas caranya, kita kenalan dulu apa itu segitiga.
Pengertian segitiga
Segitiga adalah salah satu jenis bangun datar yang terbentuk atas 3 garis yang saling berpotongan. Tiga garis ini kemudian disebut sebagai tiga sisi segitiga. Segitiga juga terbentuk dari tiga titik sudut yang letaknya tidak segaris kemudian titik-titik itu bisa dihubungkan dengan garis lurus.
Sifat-sifat segitiga
Berikut ini adalah sifat-sifat segitiga secara umum:
- Jumlah sudut-sudut pada segitiga adalah sebesar 180o.
- Sudut terbesar dalam segitiga selalu menghadap ke sisi terpanjang.
- Jumlah dua sisi segitiga selalu lebih panjang dari pada panjang sisi segitiga lainnya.
- Sudut terkecil dalam segitiga selalu menghadap ke sisi terpendek.
Ada banyak jenis segitiga, penggolongan ini didasarkan pada panjang sisi dan besar sudutnya.
Jenis-jenis segitiga
Berikut ini adalah penggolongan jenis segitiga berdasarkan panjang sisi, sifat, dan besar sudutnya:
Macam segitiga berdasarkan panjang sisinya
Berdasarkan panjang sisinya, segitiga dibagi menjadi:
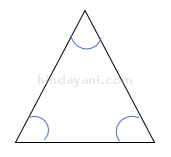
- Segitiga sama sisi
Yaitu segitiga yang tiga sisinya sama panjang.
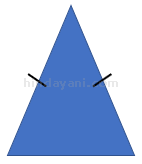
- Segitiga sama kaki
Yaitu segitiga yang dua sisinya sama panjang. Sedangkan sisi yang lain tidak, bisa lebih panjang, bisa lebih pendek.
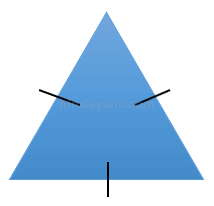
- Segitiga sembarang
Yaitu segitiga yang ketiga sisinya tak ada yang sama. Bentuknya sembarang. Sifat-sifat segitiga sembarang bisa langsung dilihat melalui gambarnya di bawah ini:
Macam segitiga berdasarkan besar sudutnya
Berikut ini adalah jenis segitiga berdasarkan besar sudutnya:
- Segitiga lancip
Ciri-ciri segitiga lancip adalah ketiga sudutnya merupakan sudut lancip.
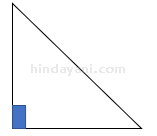
- Segitiga siku-siku
Yaitu segitiga yang salah satu sudutnya membentuk sudut 90o.
- Segitiga tumpul
Ciri-ciri segitiga tumpul adalah salah satu sudutnya membentuk sudut tumpul.
Sifat khas segitiga siku-siku, sama kaki, dan sama sisi
Berikut ini adalah beberapa sifat khas segitiga berkenaan dengan panjang sisi dan sudutnya:
- Segitiga siku-siku
Sifat khas segitiga siku-siku adalah:
- Salah satu besar sudut segitiga siku-siku adalah 90o.
- Dua sudut lainnya jika dijumlahkan menjadi 90o.
- Segitiga sama kaki
Sifat khas segitiga sama kaki adalah besar sudut segitiga sama kaki yang menghadap ke dua kakinya adalah sama besar. Sementara sudut puncaknya beda sendiri.
- Segitiga sama sisi
Sifat khas segitiga sama sisi adalah ketiga sudutnya sama besar. Besar sudut segitiga sama sisi adalah masing-masing 60o.
- Segitiga siku-siku sama kaki
Sifat khas segitiga siku-siku sama kaki adalah salah satu sudutnya siku-siku sementara dua sudut lainnya masing-masing 45o.
Sudut
Berikut ini adalah beberapa hal yang harus diketahui tentang sudut:
Pengertian sudut
Pengertian sudut adalah sebuah jarak atau daerah yang dibentuk dari dua garis yang saling berpotongan pada satu titik atau memiliki pangkal titik yang sama.
Macam-macam sudut
Berikut ini adalah macam-macam sudut:
- Sudut lancip adalah sudut yang besarnya kurang dari 90o.
- Sudut siku-siku adalah sudut yang besarnya sama dengan 90o.
- Sudut tumpul adalah sudut yang besarnya antara 90o sampai dengan 180o (lebih dari 90o dan kurang dari 180o).
- Sudut lurus adalah sudut yang besarnya pas 180o.
- Sudut refleks adalah sudut yang besarnya antara 180o sampai dengan 360o.
Mengenal sudut berpenyiku, berpelurus, dan bertolak belakang
Dalam materi sudut, kita juga mengenal istilah sudut berpenyiku, berpelurus, dan bertolak belakang. Teman-teman bisa kenalan dengan pengertian dan rumus sudut-sudut ini dalam link ulasan kami tersebut.
Baca juga: Sudut pada jajar genjang dan belah ketupat.
Rumus Cara Mencari Sudut Segitiga
Selanjutnya marilah kita mengenal beberapa rumus dan cara mencari sudut segitiga. Tapi sebelum itu, mari kita ingat materi-materi sudut di tingkat dasar dulu.
Seperti yang kita tahu, pengenalan materi tentang sudut sudah ada sejak SD. Pengenalan ini bisa dilihat melalui materi dan soal sudut kelas 3, soal matematika kelas 4 sudut, dan soal matematika kelas 5 pengukuran sudut. Di tingkat SD masih dikenalkan dasar melukis dan cara mengukur sudut saja.
Bahkan di kelas 6 pun masih dikenalkan pengukuran sudut pada arah mata angin dan antar jarum jam.
Selanjutnya, pengenalan materi sudut diperkuat di tingkat SMP. Dan untuk menyelesaikan soal sudut kelas 7 dan 8 sudah digunakan aturan segitiga. Karena di kelas ini, sudah mulai dikenalkan sudut dalam segitiga.
Memakai aturan segitiga
Seperti yang Kak Hinda paparkan sebelumnya, berikut adalah rangkuman aturan sederhana dalam segitiga yang sangat penting dipakai saat mengerjakan soal sudut di tingkat dasar:
- Jumlah sudut segitiga adalah 180o.
- Segitiga sama kaki memiliki 2 sudut yang sama besar, tepat pada sudut yang terbentuk di sisi yang sama panjang.
- Salah satu sudut yang ada di segitiga siku-siku adalah 90o.
- Segitiga siku-siku selalu memiliki salah satu sudut segitiga sebesar 90o.
- Dalam segitiga sama sisi, ketiga sudutnya sama besar, yakni 60o.
- Dalam rumus mencari sudut segitiga sembarang, biasanya akan ada minimal satu sudut yang diketahui jika ingin mengetahui sudut dalam segitiga lainnya.
- Pada segitiga siku-siku berlaku teorema pythagoras.
- Ketika ada segitiga siku-siku sama kaki, maka dua sudut lainnya (selain sudut siku-siku) besar sudut masing-masingnya adalah 45o
Selain aturan di atas, masih banyak aturan lainnya. Jadi, saat mengerjakan soal kita harus fleksibel dan paham benar mengenai sifat-sifat segitiga.
Rumus mencari sudut segitiga dengan aturan sinus cosinus
Salah satu cara yang bisa digunakan sebagai rumus mencari sudut di tingkat SMA, MA, SMK adalah dengan aturan sinus kosinus.
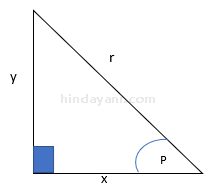
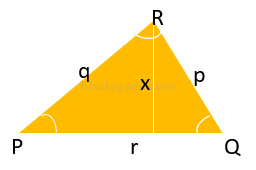
Perhatikan gambar di bawah ini untuk memahami cara menghitung sudut segitiga:
Berikut adalah bentuk sinus, cosinus, dan tangen sebagai bantuan untuk mencari rumus sudut segitiga:
- Sinus P = y/r
- Kosinus P = x/r
- Tangen P = y/x
Kak Hinda dulu menghafal aturan sinus kosinus dengan singkatan di bawah ini:
Sinkostangen demi sami desa
- Sinus = demi (depan miring)
- Kosinus = sami (samping miring)
- Tangen = desa (depan samping)
Dengan singkatan ini, aturan sinus cosinus jadi lebih mudah dihafal dan tidak terbalik-balik. Berikut penjelasannya:
- Sinus = demi (depan miring)
Artinya sinus merupakan perbandingan antara sisi depan dan miring. Sisi di depan sudut sebagai pembilang dan sisi miringnya sebagai penyebut.
- Kosinus = sami (samping miring)
Artinya cosinus merupakan perbandingan antara sisi samping dan miring. Sisi di samping sudut sebagai pembilang dan sisi miringnya sebagai penyebut.
- Tangen = desa (depan samping)
Artinya tangen merupakan perbandingan antara sisi depan dan samping. Sisi di depan sudut sebagai pembilang dan sisi sampingnya sebagai penyebut.
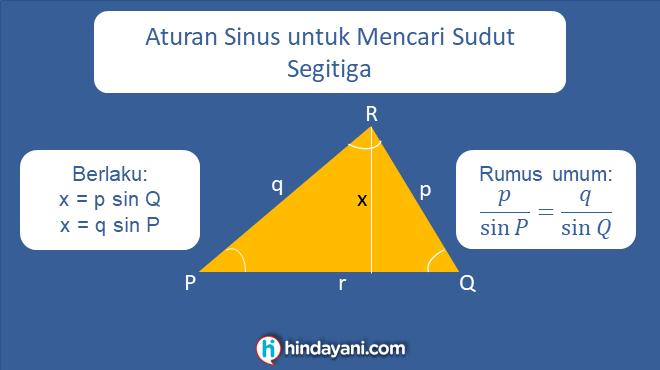
Selanjutnya, simak rumus mencari sudut segitiga sembarang dengan aturan sinus kosinus di bawah ini:
Untuk menemukan atau menghitung sudut-sudut di atas, kita butuh konsep sudut-sudut istimewa.
Sudut-sudut istimewa
Berikut ini adalah tabel sudut istimewa:
| Sudut | Sinus | Kosinus | Tangen |
|---|---|---|---|
| 30o | ½ | ½ √3 | ⅓ √3 |
| 45o | ½ √2 | ½ √2 | 1 |
| 60o | ½ √3 | ½ | √3 |
| 90o | 1 | 0 | ∞ |
| 0o | 0 | 1 | 0 |
Dari tabel sudut istimewa di atas, mengerjakan soal cara mencari sudut segitiga jadi lebih mudah.
Segitiga Kongruen dan Sebangun
Berikut ini adalah ringkasan materi kekongruenan dan kesebangunan segitiga:
Segitiga sebangun
Arti segitiga sebangun adalah saat bentuk dan jenis segitiga itu sama, dan salah satu segitiga merupakan perbesaran atau pengecilan dari skala sebesar k dari bangun segitiga yang lain.
Syarat dua segitiga dikatakan sebangun adalah:
- Pasangan sisi yang bersesuaian memiliki perbandingan yang sama.
- Sudut yang bersesuaian sama besar.
Artinya, sebelum menentukan apakah dua segitiga itu sebangun atau tidak, perlu disesuaikan dulu jenis dan bentuk masing-masing segitiga. Kemudian keduanya disesuaikan berdasarkan letak sisi dan sudutnya.
Segitiga kongruen
Pengertian segitiga kongruen adalah segitiga yang memiliki bentuk dan ukuran yang sama.
Berikut adalah syarat terbentuknya segitiga kongruen:
- Sisi-sisi yang bersesuaian sama panjang.
- Sudut-sudut yang letaknya bersesuaian sama besar.
Pada dasarnya, dua segitiga kongruen ini bisa saling menutup satu sama lain, lho!
Berikut adalah penjelasan syarat kekongruenan segitiga:
- SSS (sisi-sisi-sisi). Artinya panjang ketiga sisi dalam dua segitiga yang kongruen adalah sama besar.
- SDS (sisi-sudut-sisi). Artinya ada sudut yang sama yang diapit oleh dua sisi yang bersesuaian sama panjang.
- DSD (sudut-sisi-sudut). Artinya ada satu sisi apit dan dua sudut yang letaknya bersesuaian sama besar.
Sekarang, kita akan belajar melalui contoh soal.
Contoh Soal Sudut Segitiga
Simak beberapa contoh soal sudut segitiga di bawah ini ya!
Contoh soal mencari sudut pada segitiga dengan cara sederhana
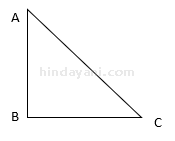
1. Contoh soal segitiga siku-siku
Besar sudut ABC pada gambar di bawah ini adalah sebesar sudut siku-siku dan sudut ACB sebesar 30 derajat. Hitunglah besar dari sudut BAC!
Jawaban:
- Sudut A + sudut B + sudut C = 180
- Sudut A = 180 – sudut B – sudut C
- Sudut A = 180 – 90 – 30
- Sudut A = 60o
Jadi, sudut BAC atau sudut A adalah sebesar 60 derajat.
2. Contoh soal segitiga sama kaki
Jika diketahui dalam segitiga sama kaki ABC, sudut A adalah sudut puncak dengan nilai 50 derajat. Hitunglah 2 sudut yang lainnya.
Jawaban:
Sudut A terletak di puncak, sehingga sudut B dan C merupakan sudut yang sama besar. Jadi cara mengerjakannya adalah;
Misal, sudut B = sudut C = x
- Sudut A + sudut B + sudut C = 180
- Sudut A + x + x = 180
- 50 + 2x = 180
- 2x = 180 – 50
- 2x = 130
- x = 130/2
- x = 65o
Jadi, sudut B dan sudut C masing-masing 65 derajat. Itulah cara menghitung sudut segitiga sama kaki yang sangat mudah.
3. Contoh untuk segitiga sama kaki
Jika diketahui salah satu sudut dari segitiga sama kaki adalah 40o, sementara 2 sudut lainnya sama besar, berapakah besar sudut yang sama besar itu?
Jawaban:
Kita tahu bahwa jumlah sudut-sudut pada segitiga adalah 180o. Itu berarti besar sudut lainnya adalah;
- 180 – 40 = 140o
- Dan karena 140 merupakan penjumlahan dari dua sudut yang sama besar, maka masing-masing sudut tersebut besarnya adalah 140 : 2 = 70o
Jadi, besar sudut lainnya masing-masing adalah 70o.
Contoh soal mencari nilai x dalam sudut segitiga
Berikut contoh soal mencari nilai x dari sudut dalam segitiga:
1. Mencari nilai x dari sudut dalam segitiga sembarang
Jika diketahui sebuah segitiga ABC dengan sudut A = 60o, sudut B = (3x – 5)o, dan sudut C = (5x + 5)o, berapakah nilai x?
Jawaban:
Sudut A + sudut B + sudut C = 180o
- 60 + (3x-5) + (5x+5) = 180
- 8x + 60 = 180
- 8x = 180 – 60
- 8x = 120
- x = 15
Jadi, nilai x nya adalah 15o. Jika Anda diminta untuk mencari besar sudut B dan C, maka jawabannya akan menjadi;
- Sudut B = 3x – 5
- Sudut B = 3.15 – 5
- Sudut B = 45 – 5 = 40o.
Jadi, sudut B adalah sebesar 40o.
2. Mencari nilai x dari sudut dalam segitiga sembarang yang punya sudut tumpul
Diketahui sebuah segitiga PQR dengan sudut P = 30o, sudut Q = 4xo, dan sudut R = 8xo. Hitunglah nilai x dan besar sudut Q dan R.
Jawaban:
Sudut P + sudut Q + sudut R = 180o (karena jumlah sudut-sudut dalam segitiga adalah 180o)
- 30 + 4x + 8x = 180
- 12x = 180 – 30
- 12x = 150
- x = 12,5
Jadi, nilai x adalah 12,5o
Sekarang, mari kita hitung besar sudut Q dan R dengan nilai x yang sudah ditemukan.
- Sudut Q = 4x
- = 4 . 12,5
- = 50o
- Sudut R = 8x
- = 8 . 12,5
- = 100o
Sudah jelas kalau jumlah sudut di segitiga itu jika dijumlahkan hasilnya 180o lagi.
3. Contoh soal mencari nilai x dalam segitiga sama sisi
Jika diketahui segitiga ABC merupakan segitiga sama sisi dengan besar sudut masing-masing adalah 2x, maka berapakah nilai x?
Jawaban:
Kita tahu bahwa pada segitiga sama sisi ada 3 sudut yang jumlah masing-masingnya sama, yakni 60o yang berasal dari 180/3 = 60. Kemudian, diketahui masing-masing sudutnya sama dengan 2x, maka kita bisa tuliskan;
- 2x = 60o
- x = 30o
Jadi, nilai x pada segitiga itu adalah 30o
4. Contoh soal mencari nilai x dalam segitiga siku-siku
Diketahui sebuah segitiga siku-siku di A dengan besar sudut B adalah 35o. Hitung nilai x jika sudut C nya adalah sebesar 5x.
Jawaban:
Kita tahu bahwa jumlah sudut pada segitiga adalah 180o, maka;
- Sudut A + sudut B + sudut C = 180
- 90 + 35 + sudut C = 180
- Sudut C = 180 – 90 – 35
- Sudut C = 55
Karena sudut C = 5x, maka
- 5x = 55
- x = 11o
Contoh soal mencari sudut dengan aturan sinus kosinus
Diketahui sebuah segitiga sembarang dengan gambar sebagai berikut:
Jika sudut Q adalah 30 derajat. Panjang PR adalah 2 cm dan panjang QR adalah 5 cm. Berapakah besar sudut R?
Jawaban:
- 2/Sin P = 5/Sin 30
- 2/Sin P = 5/½
- Sin P = 2 x ½ : 5
- Sin P = 2/10
- P = 11,5 derajat (pakai kalkulator)
Sehingga sudut R = 180 – 30 – 78,5 = 138,5 derajat
Contoh soal segitiga kongruen
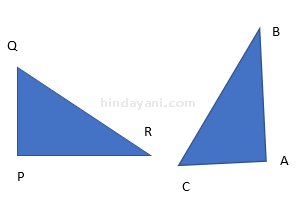
Tentukan apakah dua segitiga di bawah ini kongruen!
Jawaban:
Dua segitiga di atas kongruen, sebab:
- Sudut A = sudut P = 90o
- Panjang PQ = panjang AB
- Panjang QR = panjang BC
- Panjang PQ = panjang AC
Contoh soal segitiga sebangun
Terdapat dua segitiga ABC dan PQR. Panjang AB = ½ PQ. Sudut P dan sudut A sama-sama siku-siku. Sedangkan panjang PR dan AC sama besar. Apakah dua segitiga tersebut sebangun?
Jawaban:
Iya, sebangun. Sebab memenuhi kriteria kesebangunan. Yaitu :
- Pasangan sisi yang bersesuaian memiliki perbandingan yang sama.
- Sudut yang bersesuaian sama besar.
Contoh soal tentang kongruen dan sebangun ini mewakili contoh soal garis dan sudut beserta jawabannya. Artinya, dari soal kongruen dan sebangun ini kita mengenal tentang garis dan sudut pada segitiga.
Demikian pengertian, macam-macam, sifat, contoh soal, serta cara mencari sudut segitiga dengan mudah. Semoga cara menghitung besar sudut segitiga di atas bermanfaat ya? Kak Hinda mohon maaf bila ada salah kata.